Selection Sort

Sorting refers to the operation or technique of arranging and rearranging sets of data in some specific order in order to make it easy for us to use those data. There are many sorting algorithms used to put the elements of a list in a certain order, which can be either numerical order or any user defined order. Some of the widely used sorting algorithms are :

1. Selection Sort
2. Insertion Sort
3. Bubble Sort
4. Merge Sort

Here, I will be discussing about the Selection Sort Algorithm.

Selection Sort is a simple sorting algorithm which can be easily understood even by a beginner. In Selection Sort, an array is divided into two parts as :

1. The sorted part at the right end.
2. The unsorted part at the left end.

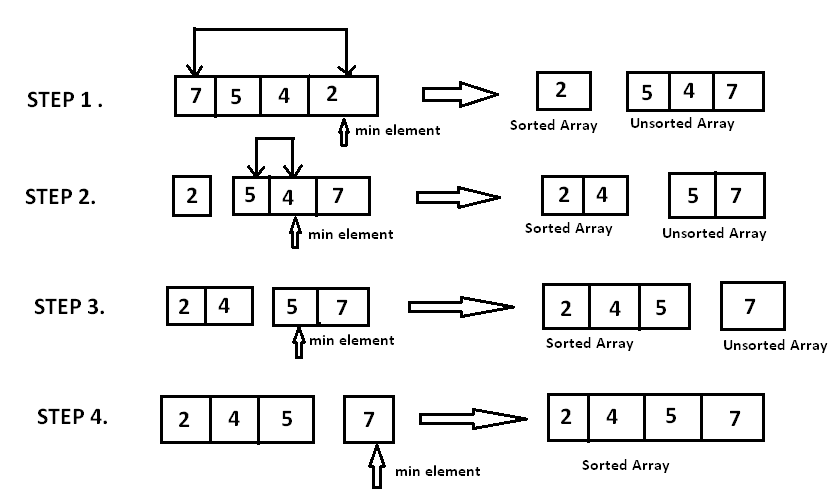
Firstly, the sorted part is empty while the entire list takes the unsorted part. The minimum element in the unsorted part is found and swapped with leftmost element in unsorted part. And then onwards that element becomes part of the sorted array. With time, the sorted part expands and the unsorted part shrinks. Finally, when the unsorted part becomes empty, we have achieved the sorted array.
The way how an array is sorted in Selection Sort Algorithm is given in the image below.

A Pseudo Code for Selection Sort

1. for i=1 to i=n-1
2. min=i
3. for j=i+1 to j=n
4.  if A[j]<A[min], then
5.    min=j
6. end for
7. if min≠i then , interchange A[i] and A[min]
8. end for

Implementation of Selection Sort in C

//arr is the name of the array to be sorted
// n is the size of the array

void SelectionSort(int arr[], int n) 
{ 
    int i, j, min; 

    for (i = 0; i < n-1; i++) 
    { 
        // Find the minimum element in the unsorted part of the array
        min = i; 
        for (j = i+1; j < n; j++) 
          if (arr[j] < arr[min]) 
            min = j; 

        // Swap the found minimum element with the first element of the unsorted array
            int temp = arr[i];  
            arr[i] = arr[min];  
            arr[min] = temp; 
    } 
} 

Complexity of Selection Sort

In first pass, finding the element with the smallest value calls for scanning all n elements; thus, n–1 comparisons are required in the first pass. Then, the smallest value is swapped with the
element in the first position. In Pass 2, finding the second smallest value requires scanning the remaining n – 1 elements and so on. Therefore,

(n – 1) + (n – 2) + ... + 2 + 1
= n(n – 1) / 2 = O(n2) 

So, we can see the time complexity of Selection Sort is the same irrespective of the original order of the elements in the given array.
When we see the space complexity, it is 0(1) as an extra variable temp is used.

Advantages of Selection Sort

• It is very simple and easy to implement.
• It can be used to sort very small data sets.

To sum up, Selection Sort is a simple sorting algorithm that is easy to understand and the knowledge on Selection Sort algorithm will help us to have a strong introduction into learning other sorting algorithms.