Linked Lists in Swift

What is data structure? It is a way of storing and organizing the data in memory. Different data structures (e.g., arrays, stacks, queues, etc.) organize data in different ways. You will look at linked lists today in terms of time and space complexity along with an example.

Linked lists are a linear data structure or collection of values where they are all stored sequentially. They are more efficient compared to arrays when it comes to insertion and deletion O(1) vs O(n) time complexity. The inefficiency in arrays is from shifting the elements after an insertion or deletion, thus O(n). In terms of space complexity, the storage is occupied in memory for arrays regardless if they contain elements or not. When appending to the end of an array and the capacity is reached, space is doubled with a new array and values copied over from the existing array. For linked lists, the space complexity is also O(n) due to the fact that you have to keep track of additional pointers, which occupy space.

Let’s look at some code now. To create a linked list data structure of integers, it can look like this:

In a linked list, you have a reference to the next node and a value for the current node.

To insert data into the ListNode, you can do the following:

In the example above, you are creating two lists: list1 and list2. It is a good idea to check if you have inserted the elements properly. So let’s do that. Recently, I learned a neat way to print out the values in the linked list from Kevin Lau and Vincent Ngo’s book on Data Structures and Algorithms in Swift. Let’s jump into the code and then I’ll explain what we did after.

In the code above, you first conform to the CustomStringCovertible protocol and second, implement the description. The description implementation uses string interpolation to print the node’s value and the next node’s value. So when you passListNode to String(describing:) initializer, the print(_:) function will use the value returned by the description. Looking at the example above, the lists are printed as follows:

Let’s extend the example and merge the two lists into one sorted list. You can assume that each list is in sorted order. There are 3 cases that you will be handling:

1. Different number of elements in the two lists
2. Same values in the lists
3. Different values in the lists

One solution can look like this:

Here’s what’s going on:

You will create temporary nodes to reference the two sorted lists and perform the following:

1. You will loop through the list as long as either of them contains a value or is non-nil.
2. In case the node in the second list is nil, you will use insertNodefunction to insert the node from the first list into the resulting linked list headNode You will see how insertNode is implemented later. You will advance the temporary pointer to the next element in the first list.
3. Repeat the similar check as step 2 but for the node in the first list and advance the temporary pointer to the next element in the second list.
4. The else will check when both elements are non-nil
5. If both values in the lists are equal to each other, then you insert both of them to the resulting linked list and advance both temporary pointers to the next node.
6. If the node in the first list is less than the node in the second list, you insert the node from the first list and advance the temporary pointer to the next node.
7. You do the opposite when the node in the second list is smaller instead.

The insertNode function is shown below:

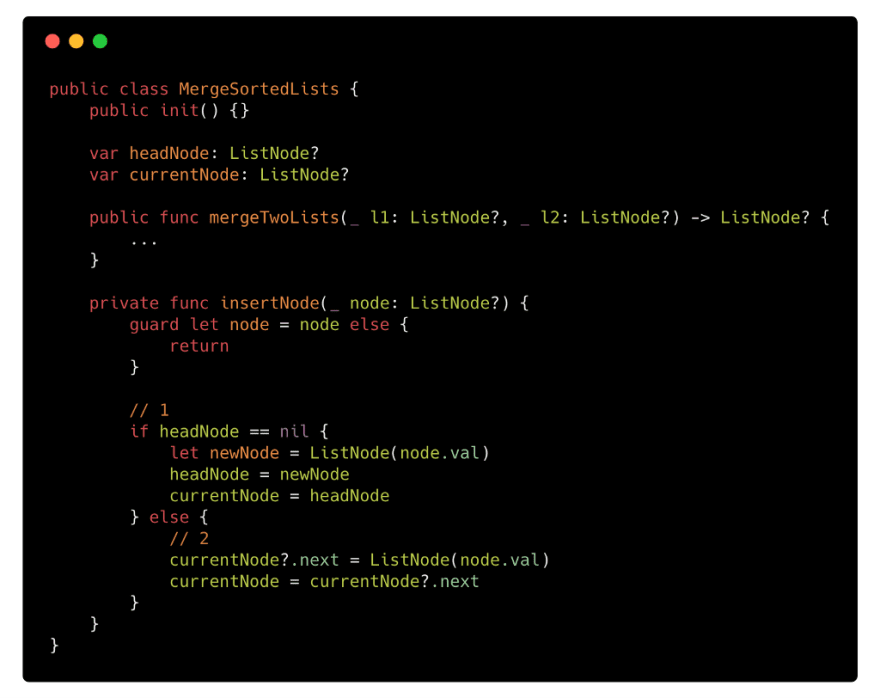
There are two parts to the insertNode logic:

1. The headNode points to the head element of the resulting linked list. So if it is nil, you will create a new node with the given value to insert into the resulting linked list. currentNode will point to the current node as you are inserting each new node.
2. If the headNode contains a node or is non-nil, a new node with the given value is created and inserted as the next node of the resulting linked list. You advance the currentNode reference to the next node.

Overall, the insertion is O(1) constant time. This is achieved by keeping track of the node that is recently inserted. Last but not least, here is the printed solution of the merged list:

Where to go from here?

Explore other topics in Kevin Lau and Vincent Ngo’s book on Data Structures and Algorithms in Swift.