Apologies for bad notation. Also, I'm not a native speaker.
I started reading this book:
I am currently reading the first chapter, which is about time complexity / asymptotic notation.
So I'm told that for an algorithm whose running time is described by the function 𝑇(𝑛) = 3𝑛³ + 2n² we have a worst-case complexity of O(𝑛³). Fine.
I'm told that I can easily prove that T(n) ≤ 5𝑛³. Fine. (I'm pretty confident in my highschool maths skills.)
Basically, I ended up with T(𝑛) ≤ 3.0...01𝑛³ for 𝑛 tends to +∞. A different value of 𝑐.
It might sound dumb that 3𝑛³ + something could be smaller than 3𝑛³ but I found this using limits.
My reasoning was that, after manipulating the inequality T(n) ≤ 𝑥𝑛³, one could end up with the following statement:
Now 𝑛 is just a positive integer constant. So let it be 1; smallest input. We end up with 𝑥 = 5. The value provided by the book.
But let's say that 𝑛 gets bigger and bigger; and eventually tends to +∞. Since 𝑛-2 would then tend to 0, we have 𝑥 tends to 3.
So T(𝑛) ≤ 𝑥𝑛³ with 𝑥 a real number that tends to 3 from upper values but is not exactly 3. In fact, it wouldn't work with 3.
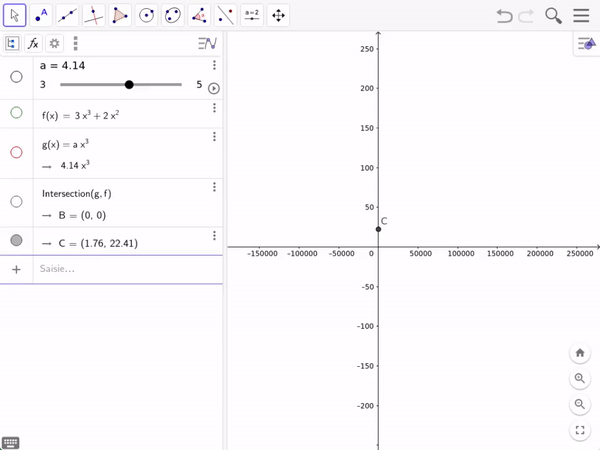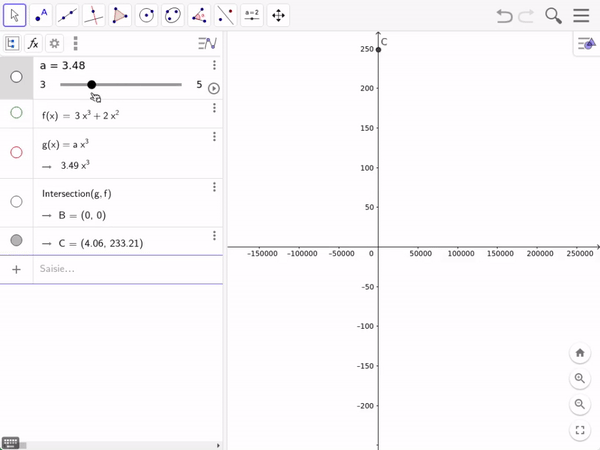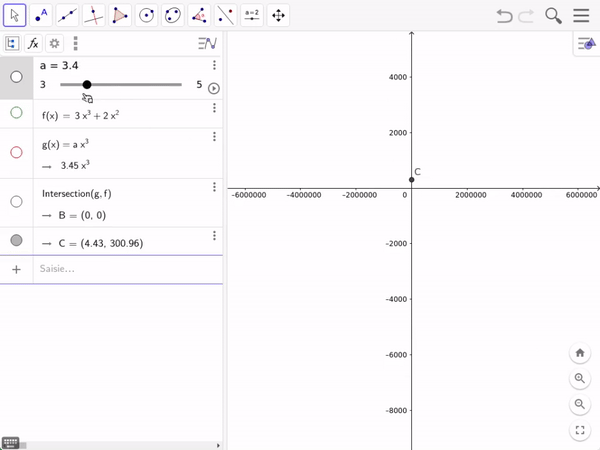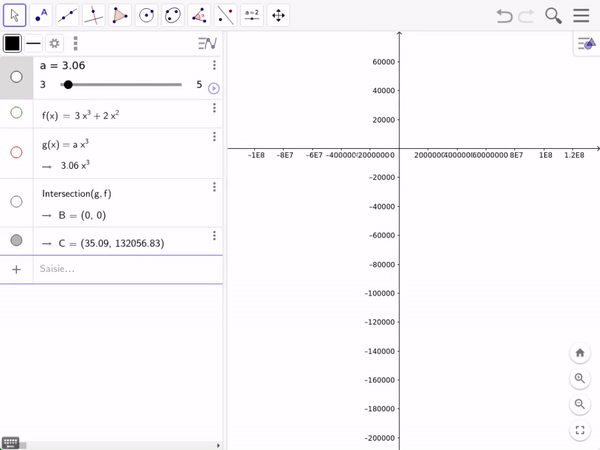
In GeoGebra
Click here if you can't see the video.
C is the point at which 𝑥𝑛³ gets bigger than T(𝑛).
My question
First of all, is my reasoning correct? Can I use this kind of reasoning when dealing with algorithms complexity? I'm pretty confident that it "holds" mathematically speaking but does it apply here?
I understand that it is not really important since we end up with the same O() but still, just curious.
Thank you.



Top comments (5)
Your understanding of limits is correct. As n approaches infinity, c can get closer and closer to 3. n³ is bigger than n² by a factor of n, which means the 2n² part gets closer and closer to negligibly.
Now, the definition of big O states:
T(n) belongs to O(n³) if there exists some finite constants c and n_0 for which every n >= n_0 satisfies T(n) <= c*n³
If n_0 is 1, then c has to be 5, as you showed.
As n_0 gets bigger, c can get closer to 3, as you also showed.
The important part is that there exists some pair of n_0 and c satisfying the requirement.
In fact, if one such pair exists, infinite pairs exist!
Hope this helped, cheers
Ok I think I get it now.
Thank you very much!^
I'm glad to hear!
If you want some practice, do have a look at a challenge I uploaded
Remove terrible bus routes (find an algorithm)
Håvard Krogstie ・ Mar 9 ・ 2 min read
The O(n²) solution is trivial, but see if you can come up with one that's O(nlog n) (Hint: sorting). I have posted a python solution in the comments, with explanations. Good luck!
There's a much more succinct and formal way of putting what I think your reasoning is:
if the limit of f(n) / g(n) is a finite number as n goes to infinity, then f is O(g).
So for example, if you're comparing
3𝑛³ + 2n²to5𝑛³, the limit of the ratio is3/5, which is a finite number, so3𝑛³ + 2n²isO(5𝑛³).On the other hand, if we compare
10n²andn, the limit is +infinity. So that means10n²is NOTO(n).Thank you for this. It doesn’t exactly help regarding my reasoning but I think your method is easier to prove that f is O(g). I didn’t know about it so thanks for introducing it to me^