Do you think algorithms are cool? Is your favorite language Javascript?

In this article, I'm gonna write how to start learning algorithms and why you need to understand algorithms as a developer, and some other topics. As our first algorithm, I'll be using insertion sort, which is easy to understand as a beginner.

Sorting Arrays

var arr = [6,3,2,1,7,4];

In javascript, it's quite easy to sort this array.

arr.sort();

Sorting in this way is a high-level approach. It's a functionality provided by Javascript. In this article, we will look at the sorting problem in an algorithmic manner.

There are plenty of algorithms to sort an array. Insertion sort is one of them. Insertion sort is a great way to start understanding algorithms. (Sorting is a fundamental operation in Computer Science)

Algorithms

An algorithm is a computational procedure that takes an input and produces some output. For example, you input an unsorted array into a sorting algorithm. Then, you get a sorted array. (That's what we are going to do here)

Algorithms are created to solve a specific computation problem. Good algorithms solve them fast and efficiently. I will explain the meaning of "good" later.

Algorithms for a Dev?

This is hard to explain. But, understanding an algorithm will indeed help you to think in a new way when you are developing something. It will help you to write code quickly. And, it lets your brain to think fast and provide you the best result. (Quora Discussion on this topic)

Insertion Sort

Let's get into the problem!

Problem: Sorting an array
Input: An array of numbers (Unsorted)
Output: Sorted array

Insertion sort is a efficient algorithm to solve the "sorting problem" in the computer world. It works exactly as how we sort a hand of playing cards.

• First, you have your set of cards on the table.
• Then, you get one and keep it in your hand.
• Next, you get another and compare it with the first one and add it into the correct position.
• Then, you get the third card and add into the correct position compared to other two cards.
• The same process continues...
• Finally you will have a sorted hand of cards.

One thing you should notice is that always the cards hold in the hand is sorted.

Insertion sort in Javascript

Let's implement what we discussed in English in Javascript. (Just 7 rules)

function insertionSort(arr) {
    for (var i = 1, len = arr.length; i < len; i++) {
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j]
            j--;
        }
        arr[j + 1] = key;
    }
    return arr;
}

Usage of the function

var arr = [3,1,5,6,2];
console.log(insertionSort(arr));

Explained...

• We send an unsorted array into our function.
• for (var i = 1, len = arr.length; i < len; i++) makes a loop from the index 1 to len - 1. So, we don't use the first element for the loop.
• key = arr[i] saves the value in a variable. key is the "card" which we are going to insert into our hand.
• j = i - 1, initial j is i - 1, which is the index right before i.
• while (j >= 0 && arr[j] > key), loops through the cards in our hand if the value of index j is greater than our key.
• arr[j + 1] = arr[j], shifts the element we checked (index j) one time to the right.
• j--, decreases j. So, we can examine the previous element. If j < 0, the while loop ends, as we don't have more cards in our hand.
• arr[j + 1] = key, inserts our card into the correct position. (j + 1 is used because, inside the while loop, j decreases one more time than it should)

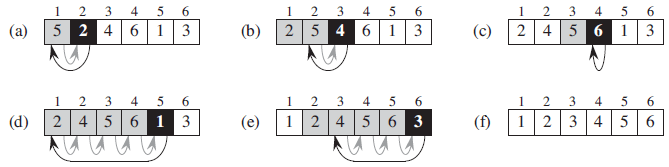
Loop by loop with the example...

When starting to understand an algorithm which has loops, the best way is to go loop by loop with an example. It gives you an idea what the algorithm really does.

Let's take the first loop.

• [3,1,5,6,2] is our unsorted array. (5 elements, index 0 to 4)
• for loop loops from the index 1 to 4 ([1,5,6,2] elements)

First for loop

• i is 1
• key is 1
• j is 0
• arr[j] is 3
• arr[j] > key

So, we shift the element 3 one time to right. Now we have the array [3,3,5,6,2].

• j--. Now j is -1. j < 0. So, while loop terminates
• arr[j + 1] = key equals arr[0] = 1.

After the first loop we have the array [1,3,5,6,2]

We just inserted the card "1" into its correct position in our hand (We only had [3], in our hand)

Second for loop

• i is 2
• key is 5
• j is 1
• arr[j] is 3
• arr[j] < key
• while loop doesn't run

We have the same array [1,3,5,6,2] after the second for loop.

Third for loop

• i is 3
• key is 6
• j is 2
• arr[j] is 5
• arr[j] < key
• while loop doesn't run

We have the same array [1,3,5,6,2] after the second for loop.

Forth for loop

This is the interesting part.

Now we have [1,3,5,6] (sorted) in our hand. 2 is the element we are examining. We are going to insert it to the correct position.

• i is 4
• key is 2
• j is 3
• arr[j] is 6
• arr[j] > key
• while loop runs
  • Shifts 6 one time to right. Now we have [1,3,5,6,6]
  • 5 > 2, shifts 5 one time right. [1,3,5,5,6]
  • 3 > 2, shifts 3 one time right. [1,3,3,5,6]
  • 1 < 2, that's the 2's position! Insert it after 1. Now we have [1,2,3,5,6].

We just sorted our array using insertion sort!

Analyzing Algorithms (Thinking like a computer scientist :D)

When we have multiple algorithms for the same problem (Ex: There are insertion sort, merge sort, selection sort, etc. for the "sorting problem"), we will need to analyze each algorithm and find the best one.

In general, analyzing an algorithm means predicting the resources an algorithm requires. There are facts like memory, bandwidth, computer hardware usage, etc. Most often computational time is used to analyze an algorithm. The more time it takes, the more bad it is. There are many things to consider when analyzing an algorithm.

In this article, I'll explain a simple way of analyzing an algorithm we create. For this task, you will need to understand these concepts.

• What if a computer had an instruction to sort an array? So, it just takes a single command. (This is not arr.sort() in Javascript. .sort() in Javascript uses insertion sort to sort an array, if the number of elements are less than 10). In real computers, we only have instructions for arithmetic, conditionals, data movement, etc.
• We will be using the RAM model, which executes instructions one by one, and no concurrent operations.
• Sorting thousand numbers using insertion sort takes time than 3 numbers. In modern computers, the difference can be negotiable. But, if we had billion, it matters.
• Insertion sort takes more time to sort depending on how nearly the input array is sorted.
• The time taken by insertion sort depends on how much input you have (input size), and how much steps you have for each execution.

Worst and Best cases

For insertion sort,

Best case occurs when the input array is already sorted. For the best case, the running time can be expressed as an + b, where a and b are constants and n is the size of input.

Worst case occurs when the input array is sorted in the descending order. For the worst case, the running time can be expressed as an(2) + bn + c, which is a quadratic function.

The mathematical equations are created using the concepts like input size and running time, which are not that hard to understand. But, I won't include the mathematical calculations here.

What's next?

If you read up to here, I'm really happy! Here are some things you can do.

• Follow a tutorial! (Khanacedemy would be fine)
• Read a book on algorithms. (I recommend this one.)
• Continue with Python. Then, recreate it with Javascript. When you are learning algorithms, Python is the best language that you can write the code easily. If you like to enjoy algorithms more, convert it to Javascript (Like me :) )

Liked the article?

If you liked the article and if you would like to help me, I created new website, Hyvor Groups, which is a place to create groups, join them, and post and share posts. Please join Hyvor Groups and share your work, ask questions, and share the website with your friends.

Related groups

1. Web Devloper's Group
2. PHP Group
3. Javascript Group

Feel free to create your own group!

Thank you!