Hope you read my previous article on the selection sort, and how it is similar to Insertion sort.
If not, check out this article below.
We will see the Merge Sort today.
Merge Sort is a divide and conquer sorting algorithms, which uses recursion to sort.
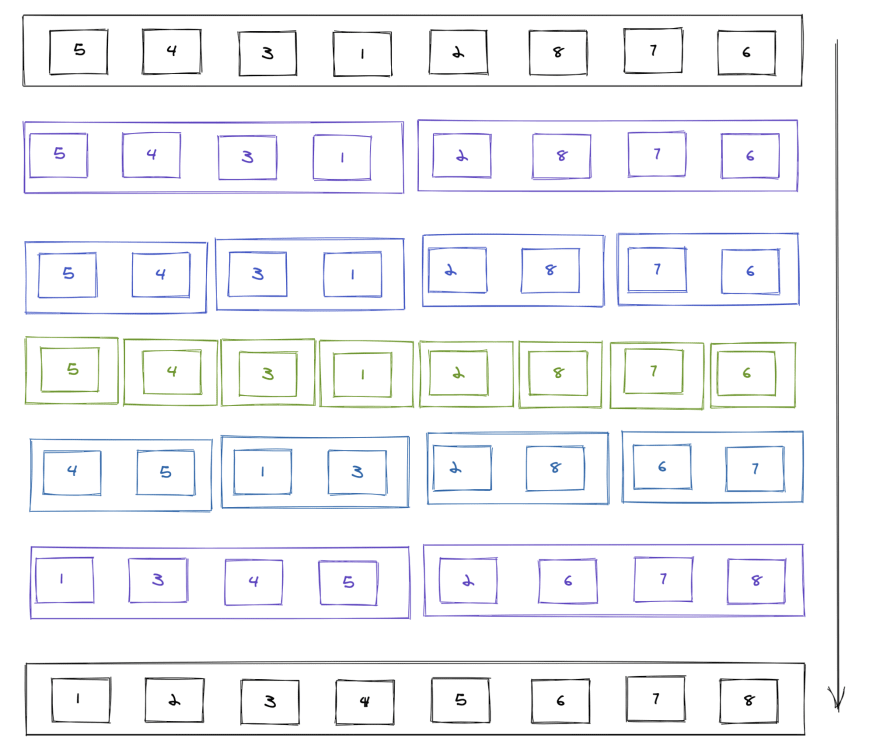
Here is a pictorial representation of how it works.
(Top -> Bottom)
In the above diagram, we are dissecting the elements of array based on a pivot value (depending on the length of the array).
Since the dissection happens back to back due to recursion, we would need a base condition. Here our base condition is to return the input if the "input.length" is less than or equal to 1.
Once the elements are dissected, the sorting happens.
Here we compare the values of 2 arrays dissected starting from the index "0". If the value on the left found to be smaller, we will push that element to the result array and increment the counter on the left array (only), same goes to the array on right.
We do it repeatedly until the counter value reaches the array length.
In the end, there will be one element either in right or the left array which needs to be pushed to the result (the largest element), so we concatenate that value while returning the result.
Video reference (Start from 3:08)
Below is the implementation in JavaScript for the Merge Sort algorithm
Here is the result.
Hope you find this helpful.
Please share your feedback, will see you again.
Thanks,
Sudharsanan Ravichandran





Top comments (3)
The critical insight for merge sort is that all sequences of length <= 1 are correctly sorted.
It is also worth noting that the algorithm presented here is a 'top-down merge sort'.
There is also a 'bottom-up merge sort'.
In the bottom up case you skip the sub-division step and just extract two lists of length one from the input, merge, and repeat.
The top-down approach does more work to allow an in-place sort.
The bottom-up approach does less work, but requires more temporary space.
There are also other variations on merge sort.
Merge sort is one of the basic families of sort algorithm and well worth understanding.
Thanks for sharing your insights, could you please help me with resources if you happen to have any?
Wikipedia provides a reasonable overview of both top-down and bottom-up, and talks about natural merge sorts, and exploiting accidental in-order runs.
I don't see any errors here so it's probably reasonably solid for a wikipedia article.
(Although I haven't gone over it with a fine comb, so I may have missed something)
en.wikipedia.org/wiki/Merge_sort#A...
Prinston gives a nice analysis of both top and bottom, and compares with quicksort.
cs.princeton.edu/courses/archive/s...
Quicksort is quite similar to top-down merge sort, so it's useful to understand the differences.