Container with Most Water

This post originally appeared on steadbytes.com

A solution and, importantly, a proof for LeetCode Problem 11 - Container with Most Water.

This problem intrigued me as, unlike many "LeetCode-esque" problems, little advanced or specific algorithms theory is required for an optimal $O(n)$ solution. That is, there was no algorithmic or mathematical trick that one needed to solve the problem. Instead, the solution relies on a subtle insight that leads to a relatively simple algorithm. This, in my opinion, is the real skill behind designing algorithms that can be gained from "LeetCode-esque" problems - as opposed to re-writing the same handful of algorithms over and over again.

The algorithm itself is fairly simple to understand intuitively, however understanding why it works is less so. In this article, I present my solution (which is essentially identical to many others you may find) and provide a formal proof of the key insight; something I have been unable to find a satisfactory example of.

I encourage the reader to visit LeetCode and attempt to solve the problem before reading further.

Problem

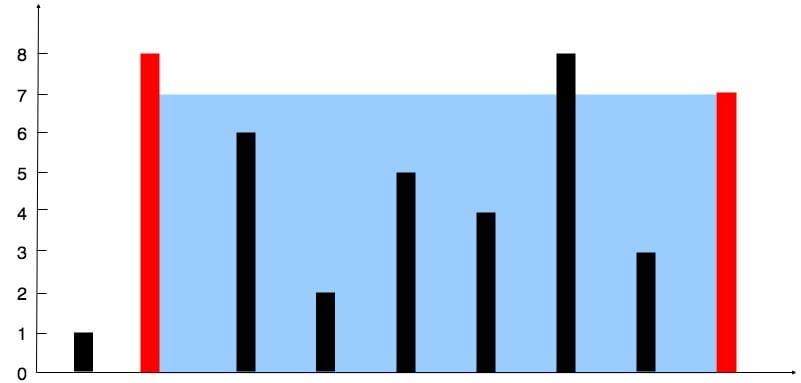
Given $n$ non-negative integers $a_{1}, a_{2}, ..., a_{n}$ , where each represents a point at coordinate $(i, a_{i})$ . $n$ vertical lines are drawn such that the two endpoints of line $i$ is at $(i, a_{i})$ and $(i, 0)$ . Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and $n \geq 2$

— https://leetcode.com/problems/container-with-most-water

Example:

Input: [1, 8, 6, 2, 5, 4, 8, 3, 7]
Output: 49

Solution

impl Solution {
    pub fn max_area(height: Vec<i32>) -> i32 {
        let mut l = 0;
        let mut r = height.len() - 1;
        let mut max_area = 0;

        while l < r {
            let width = (r - l) as i32;
            if height[l] < height[r] {
                max_area = max(max_area, height[l] * width);
                l += 1;
            } else {
                max_area = max(max_area, height[r] * width);
                r -= 1;
            }
        }
        max_area
    }
}

Using two pointers, the entire array of heights is processed in a single pass from both ends simultaneously; thus $O(n)$ . On each iteration, the area of the container between l and r is calculated and the lower-heighted of the two is moved towards the other. Either can be moved in the case that i == j (so long as it is consistent) - here I chose to move r. The maximum are

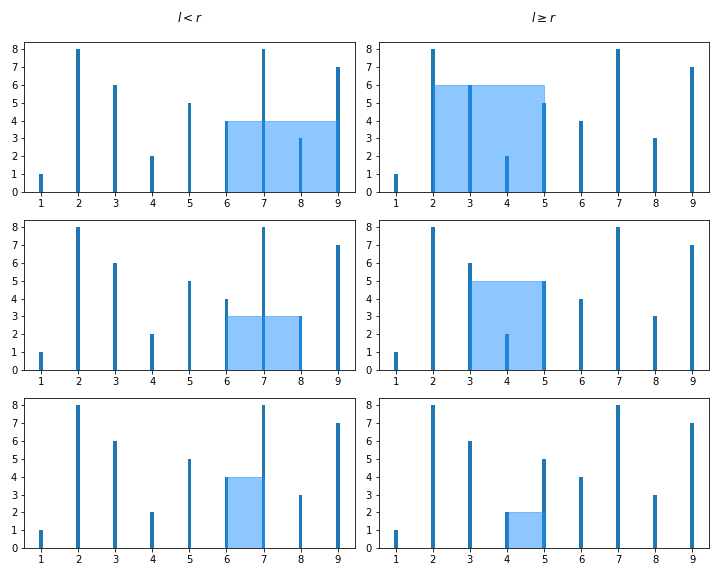
The key idea is that for any two positions of l and r, the corresponding container area is larger than that of any container produced by moving the pointer with the larger height towards the other. All such containers therefore need not be considered.

Proof

Definitions

Let $a_{i}$ be the height of the line at index $i$ and $W(i, j)$ , $H(i, j)$ , $A(i, j)$ be the width, height and area, respectively, formed by the container between $a_{i}$ and $a_{j}$ :

Loop Invariant

The "key idea" previously mentioned.

Hypothesis: For any $i, j$ where $i< j$ , $A(i, j)$ is greater than the area produced by moving either $j$ towards $i$ if $a_{i} < a_{j}$ or $i$ towards $j$ otherwise:

When $a_{i} < a{j}$ :

The container width, by definition, has decreased since $j$ has moved closer to $i$ :

Since $a_{i} < a_{j}$ , there are two cases for the height of the container $H(i, j^\prime)$ :

Thus,

The same process applies to the case where $a_{i} > a_{j}$ .

Termination

Since the result is returned immediately after exiting the single while loop, proving termination is equivalent to proving the termination of this loop.

The while loop terminates when the expression l < r evaluates to false:

while l < r {
    // ...
}
// l >= r

The loop contains and if-else expression which defined the only two possible code paths:

while l < r {
    let width = (r - l) as i32;
    if height[l] < height[r] {
        max_area = max(max_area, height[l] * width);
        l += 1; // 1.
    } else {
        max_area = max(max_area, height[r] * width);
        r -= 1; // 2.
    }
}

The lines indicated 1. and 2. are the only lines that affect the while loop condition - calculations of width and max_area do not alter the values of l and r. Therefore, there are two relevant cases:

while l < r {
    if some_condition {
        l += 1;
    } else {
        r -= 1;
    }
}

Either, l is incremented or r is decremented. Since l is initialised to 0 and r to the length of the height array the two must converge and thus the while loop must terminate.

More formally, with respect to pointers $l$ and $r$ , each iteration of the while produces new values of $l$ and $r$ as follows:

Since $l$ and $r$ are initialised to $0$ and $n$ , where $n > 0$ , the two values converge and thus loop exit condition $l < r$ is satisfied.