The debate of whether being good at math makes for a great programmer is as old as the tech industry itself. Opinions are wildly polarizing ranging from completely discarding mathematics as irrelevant to claiming a math or CS degree to be an absolute prerequisite for software engineering.
As always, the truth is somewhere in the middle of the spectrum. This write-up aims to give a practical example of how math can inform programming.
Disclaimer
No doubt, there are niche areas of programming that require unique skill sets and/or specialized education. For example: computer graphics, image/video processing, cryptography, machine learning, modeling physical processes, etc. Some of these are closer to scientific research than practical programing and may indeed require academic training.
As opposed to the domains above, general purpose software engineering is all about mundane business applications: desktop, mobile, and web applications. It's not rocket science.
Practical Example
Consider a practical coding example that most developers encounter early on in their career. The task is to render a human-friendly rounded number with a unit prefix, for example:
- 350,000 → 350K
- 1,500,000 → 1.5M
- and so on.
This algorithm is everywhere: from financial charts to YouTube likes.
Here's a recent Tweet from the Laravel community on the topic.
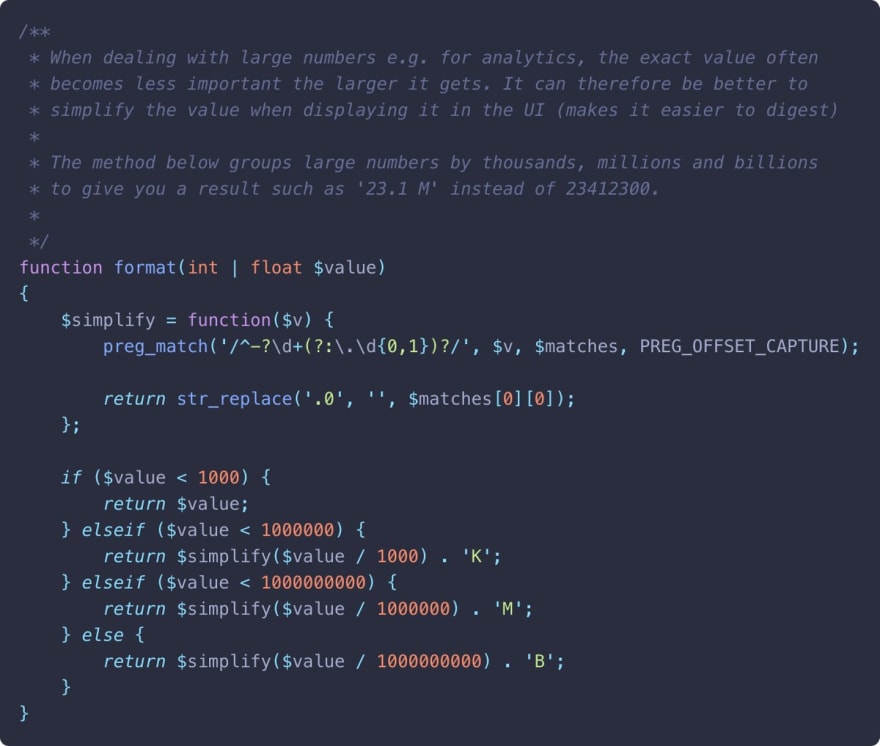
 Matt Kingshott@mattkingshott
Matt Kingshott@mattkingshott 🔥 #Laravel Tip: When dealing with large numbers e.g. for analytics, the exact value often becomes less important the larger it gets. It can therefore be better to simplify the value when displaying it in the UI…14:40 PM - 01 Feb 2022
🔥 #Laravel Tip: When dealing with large numbers e.g. for analytics, the exact value often becomes less important the larger it gets. It can therefore be better to simplify the value when displaying it in the UI…14:40 PM - 01 Feb 2022
Code snippets are in PHP, but they translate to any high-level programming language, such as JavaScript.
Basic Implementation
A straightforward implementation would be to handle conversion to each unit of measurement individually, checking for all supported integer ranges.
The initial implementation:
function formatNumber(
int|float $number,
int $precision = 1
): string {
if ($number < 1000) {
$result = $number;
$unit = '';
} else if ($number < 1000000) {
$result = $number / 1000;
$unit = 'K';
} else if ($number < 1000000000) {
$result = $number / 1000000;
$unit = 'M';
} else {
$result = $number / 1000000000;
$unit = 'B';
}
return (string)round($result, $precision) . $unit;
}
This algorithm has several disadvantages.
One of the biggest drawbacks is having to modify source code to register new unit prefixes; they're hard-coded in the implementation. It's not universal enough to serve as a reusable library.
Another disadvantage is the duplication of 1000s across the implementation. You need to type in 0s very carefully to not make a mistake.
Let's try to overcome these limitations.
Generalized Implementation
The next iteration in the evolution of our algorithm accepts units as input and loops over them. It now works with any number of unit prefixes!
The improved implementation:
function formatNumber(
int|float $number,
int $precision = 1,
int $base = 1000,
array $units = ['K', 'M', 'B']
): string {
$result = $number;
$unit = '';
$unitCount = count($units);
for ($unitIndex = 0; $unitIndex < $unitCount; $unitIndex++) {
if ($result < $base) {
break;
}
$result = $result / $base;
$unit = $units[$unitIndex];
}
return (string)round($result, $precision) . $unit;
}
For a fixed set of units, this loop-based approach is equivalent to the original implementation, just more flexible.
Now that the base factor 1000 isn't hard-coded anymore, both decimal and binary units are supported, for instance:
formatNumber($number, base: 1024, units: ['KiB', 'MiB', 'GiB'])
We haven't considered algorithmic complexity yet, let's see where the implementation stands. The time complexity in Big O notation is O(n), where n is the number of unit prefixes.
The algorithm is pretty flexible, short, and easy to understand and maintain. But can the linear complexity be improved upon?
Optimized Implementation
Making further improvements requires completely rethinking the approach. Ideally, the algorithm should be independent of the input size. That means there should be no loop at all.
Take a closer look at the algorithm. What does each iteration do? It calculates intermediate results, building upon results of the previous iteration. But can we jump to the solution immediately? That's where math comes in.
Each iteration gradually converts the input number to ever larger units. The number of iterations corresponds to the largest applicable unit. Each division essentially increments the power of the base used in the conversion.
We can convert the input number to the respective unit by dividing it by the base raised to the power of the unit. How do we determine the base power? We can use logarithms to calculate the power of the base yielding the input number. Then round it down to the closest integer. That also gives us the sequential index in the units array (to be adjusted for zero-based indexes). And voilà, we get both the converted number and its unit prefix!
The final implementation:
function formatNumber(
int|float $number,
int $precision = 1,
int $base = 1000,
array $units = ['K', 'M', 'B']
): string {
$unitCount = count($units);
$power = (int)floor(log(abs($number), $base));
$power = min($power, $unitCount);
$result = $number / pow($base, $power);
$unitIndex = $power - 1;
$unit = $units[$unitIndex] ?? '';
return (string)round($result, $precision) . $unit;
}
Expression min($power, $unitCount) limits the algorithm to units whose prefixes have been defined, i.e. the conversion stops at the largest unit.
Note that abs($number) makes it work for negative numbers, support of which all previous implementations have overlooked.
The time complexity of the algorithm is O(1) as it completes in a fixed time regardless of the number of unit prefixes. Absence of conditionals and loops also improves other code quality metrics, namely Cyclomatic complexity and NPath complexity.
Conclusion
Math is by no means required in day-to-day coding. In practice, even if it does come down to advanced math, one would use an existing library provided by the rich OSS ecosystem of their tech stack.
However, middle school algebra and geometry do occasionally come in handy in programming. Mathematics underlies performance optimizations of certain otherwise resource-intensive algorithms: proficiency in the subject allows to understand and implement these optimizations.
Happy programming, with or without math!






Top comments (2)
Useful articles. Thank you.
completely agree with the conclusion you made.