Photo by Roman Mager on Unsplash
During a semester in college I took a subject called "Discrete Mathematics". The lecturer decided to split the class in groups. Each group consisted of 2 or 3 students. They were meant to do expositions about a particular subject assigned by the lecturer.
In the group I was on (we were only two, actually), we were assigned with the subject of recurrency relations. According to Wikipedia, this is:
an equation that recursively defines a sequence or multidimensional array of values, once one or more initial terms are given: each further term of the sequence or array is defined as a function of the preceding terms.
In other words, a recursive function ;)
A perfect situation to explain this concept with code :D
Hanoi Towers
Do you remember this toy?
The famous Hanoi Towers. The game consists of moving every disk from the first pole to the last one (from left to right or viceversa) in the least amount of steps possible. The rules are that a bigger disk cannot be over a smaller one and you can move only one disk at the time. Something like this:
This problem has an algorithm that solves it, it goes like this:

Where n is the amount of disks in the problem.
Let's code that
Let's use Python to write that algorithm. It's something like this:
def hanoi(n):
if n <= 1: return 1
else: return 2 * hanoi(n-1) + 1
So if we have 4 disks...
>>> hanoi(4)
15
Good. It works. Let's give it a few tries
>>> hanoi(5)
31
>>> hanoi(10)
1023
>>> hanoi(40)
1099511627775
Looks pretty good. Now I know how many moves it will take me if I'm using 40 disks (btw, this is gonna take you 10460 years, never try this at home). But what if I have 7000?
>>> hanoi(7000)
Traceback (most recent call last):which
File "<stdin>", line 1, in <module>
File "<stdin>", line 3, in hanoi
File "<stdin>", line 3, in hanoi
File "<stdin>", line 3, in hanoi
[Previous line repeated 994 more times]
File "<stdin>", line 2, in hanoi
RecursionError: maximum recursion depth exceeded in comparison
Oh... It seems this is not performant enough. Of course you could "solve" this just increasing the maximum recursion depth in Python (with sys.setrecursionlimit(n)), but it's a much better idea to optimize this.
Optimizing
There are several ways to solve recurrence relations, one of them is iteration. It consists of solving the operation step by step and deducting the non-recursive equation from the process. First we try to solve a given value:
Then, from the last line, we can deduce an equivalent equation:
If you notice, t(4) = 8 + 7 is the same as t(4) = 2^(4-1) + (2^(4-1) - 1), that's why it's our initial statement. But now we have solved the recurrence relation, let's use that in our code.
def better_hanoi(n):
return 2**n - 1
And then...
Now we know how many steps will take to solve it with 7000 disks (probably the lifetime of the universe, several times).
Conclusion
We have optimized a small algorithm with concepts of discrete mathematics, this is just to give a little insight on how we can benefit of such simple concepts to build better programs.




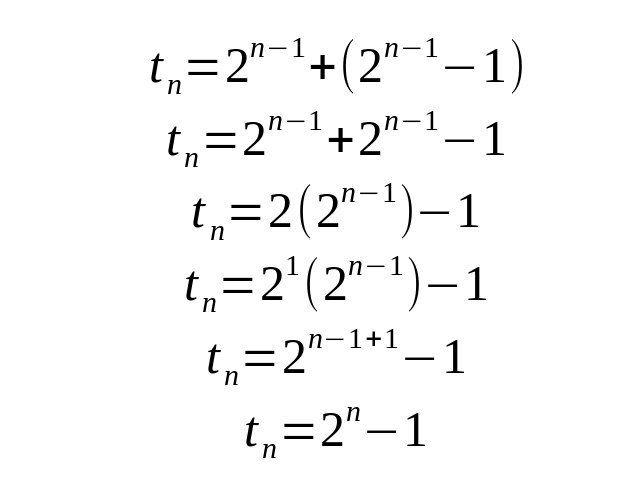


Top comments (7)
I don't follow how you deduce
t(n) = 2^(n-1) + (2^(n-1) - 1)fromt(4) = 8 + 7Can you expand on that?
Given this expression:
t(4) = 8 + 7We can deduce this:
t(4) = 2^(4-1) + (2^(4-1) - 1)Therefore, that expression can be abstracted to:
t(n) = 2^(n-1) + (2^(n-1) - 1)Given the previous expression, when
n = 4thent(4) = 8 + 7.Of course, to achieve this expansion through deduction, you'd need to compare it with other values of
nalso.I hope this solves your doubt :)
Not really, my math is rusty and I'm probably missing some required knowledge for this.
Let me rephrase my question:
What is the deduction process by which
8+7becomes2^(4-1) + (2^(4-1) - 1)? This is the part I don't understand.To understand that deduction process, let's solve this with more values of
n.Given the following equation:
t(n) = 2^(n-1) + (2^(n-1) - 1). We'll solvet(n)forn=1,n=2,n=3andn=4.t(1) = 2^(1 - 1) + (2^(1 - 1) - 1)t(1) = 2^(0) + (2^(0) -1)
t(1) = 1 + (1 - 1)
t(1) = 1 + 0 = 1
We can't deduce anything from
n=1only, let's try withn=2.t(2) = 2^(2 - 1) + (2^(2 - 1) - 1)t(2) = 2^(1) + (2^(1) - 1)
t(2) = 2 + (2 - 1)
t(2) = 2 + 1
t(2) = 3
Hm, ok, we have a relation here, where the value we pass is
2, and the value we get is3. And if we pass1, we get1. Maybet(n) = n+(n-1)? Let's keep going, two values are not enough.t(3) = 2^(3-1) + (2^(3 - 1) - 1)t(3) = 2^(2) + (2^(2) - 1)
t(3) = 4 + (4-1)
t(3) = 4 + 3
t(3) = 7
Wait, our relation (
t(n) = n+(n-1)) doesn't apply here. But the relation of3and7, seems familiar somehow. Let's keep going.t(4) = 2^(4-1) + (2^(4-1) - 1)t(4) = 2^(3) + (2^(3) - 1)
t(4) = 8 + (8 - 1)
t(4) = 8 + 7
t(4) = 15
Wait, this look like
2^n - 1. It applies to our previous values. If we try withn=5then...t(5) = 2^(5-1) + (2^(5-1) - 1)...
t(5) = 16 - 15
t(5) = 31
It works. Now you see that the function
2^n - 1applies to the relations of our previous values (t(1) = 1,t(2) = 3,t(3) = 7,t(4) = 15,t(5) = 31).As to why
8 + 7, thanks to the previous exercise, we can now deduce that2^(4-1) = 8and therefore2^(4-1) - 1 = 7. In the post, as soon as I got rid oftin8t + 7, I tried to deduce the values of8and7and got that formula (2^(4-1) + (2^(4-1) - 1)).Let me know if this helps to make myself clear.
Not quite... Solving for the given equation
t(n) = 2^(n-1) + (2^(n-1) - 1)is straight forward. Nothing complicated about replacingnwith an actual number. This is not the source of my confusion.I am asking how you get to the given equation in the first place. As in, you start with
8+7and a few steps later it's2^(n-1) + (2^(n-1) - 1)I'm going to use your example with
t(4)from the previous comment, but reverse, because that is the process I am trying to figure out.t(4) = 8+7// factored recursive hanoi down to this. cool, makes sense.t(4) = 8 + (8 - 1)// ok I guess, but why?t(4) = 2^(3) + (2^(3) - 1)// Math makes sense, but why did we decide to represent 8 as an 2 to the 3rd? Is the goal to find exponential representations?t(4) = 2^(4-1) + (2^(4-1) - 1)// Why on earth did we decide3is better represented as4-1??From here, factoring
2^(4-1) + (2^(4-1) - 1)down to2^n-1makes perfect sense.The source of my frustration here is not so much the math, but why the choices were made to eventually turn
8into2^(4-1)I would really appreciate shedding some light on that part specifically.
Hold that thought right there. The reason why we use
4-1instead of3is to represent the value ofnin the formula, so we can writen-1. Because in that example,n = 4.If you notice in my previous comment, my goal was not simply to solve the equation with several values of
n, but to show how the result and the parameters of the function relate each other.The goal of the deduction process is to find the function that solves these relations:
t(1) = 1 + 0 // same as 2^(1-1) + (2^(1-1) - 1)t(2) = 2 + 1 // same as 2^(2-1) + (2^(2-1) - 1)
t(3) = 4 + 3 // same as 2^(3-1) + (2^(3-1) - 1)
t(4) = 8 + 7 // same as 2^(4-1) + (2^(4-1) - 1)
t(5) = 16 + 15 // same as 2^(5-1) + (2^(5-1) - 1)
That way you can find a function that solves for every value of
n. Please let me know if I now made it clear.Very interesting article!