The Transformer Architecture [1] introduced by Vaswani et al, is based on attention mechanism and overcomes the challenges faced in recurrence. In continuation to the last blog 'Let's pay some Attention!', let's delve deeper into Attention Mechanism.
Recurrent Neural Networks or RNNs were introduced to handle the sequential data but optimisation tends to take longer in case of RNN due to :
- The number of iterations or steps in gradient descent is higher in recurrence.
- There are several sequential operations which can not be parallelised easily.
Multi-Head Attention
Let's do a quick recap of the attention mechanism we understood in the last blog.
We have some key - value pairs and a query. We compare the query to each key and the key with the highest similarity score is assigned the highest weight. To generate an output, we now take a weighted combination of the corresponding values.

In the flow chart above, we feed the Value (V), Key (K) and Query (Q) into a linear layer with, say 3, projections each of V, K and Q. Then we compute a scalar dot product attention of each of the projection, one head per linear layer, thus we get 3 heads of scaled dot product attention . Now we concatenate these heads into one and feed the concatenated output into a linear layer which then outputs the multi-head attention.
In the case of Multi-Head Attention, we compute multiple attentions per query with different weights.
Masked Multi-Head Attention
When decoding the output from encoder, an output value should only depend upon previous outputs and not the future outputs. Thus, to ensure that future values have zero attention, we mask them. We define masked multi-head attention as the multi-head attention where some values are masked and the probabilities of masked values are nullified to prevent them from being selected.
Mathematically, as illustrated below, Masked Multi-Head Attention is calculated by the addition of 'M', a mask matrix of zeroes and negative infinity to the transpose of query.
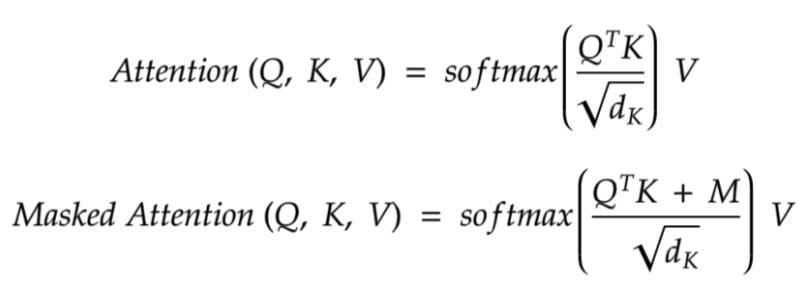
QT : Transpose of Query
K : Key
V : Value
dk : Dimensionality of each key
M : Mask Matrix of 0s and -∞
Layer Normalisation
In the performance of Transformer, layer normalisation [2] introduced by Lei Ba et al. plays a key role.
The interdependency of weights and their constant change during computation is eliminated with the help of layer normalisation. Normalisation ensures that regardless of how we set the weights, the output of a layer have a mean of '0' and a variance of '1'. Thus, the scale of these outputs is going to be the same leading to faster convergence.
While in case of layer normalisation, normalisation is at a layer level whereas for batch normalisation, it is performed for one hidden unit but by normalizing across a batch of inputs.
Understanding Complexities
In a self attention network, a layer consists of 'n' positions. For each position, the dimensionality is given as 'd'. Computation in one layer is going to be of order 'n2' because for every position we attend to every other position. For each such pair, we are going to compute an embedding of dimensionality 'd'. Thus, the complexity of every layer is 'n2d'.
In this blog we covered multiple topics associated with the concept of Attention.
References :
[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17). Curran Associates Inc., Red Hook, NY, USA, 6000–6010.
[2] J. L. Ba, J. R. Kiros, and G. E. Hinton. Layer normalization. arXiv preprint arXiv:1607.06450,
2016.



Top comments (0)