Solution Developed In:
The Question
For this article we will be covering Leetcode's '329. Longest Increasing Path in a Matrix' question. A Dynamic Programming Graph Question.
Question:
Given an
m x nintegersmatrix, return the length of the longest increasing path inmatrix.
From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].
Explaining The Question
This Question is rated Hard. Which I believe is entirely accurate, so long as you have solid foundations in Graph Theory and it's applications. As well as ideally being skilled in either DFS or BFS algorithms as well as having knowledge in Topological Sort you will be able to solve this problem.
Now this is a Dynamic Programming Question. Which we all love 😉. This question should feel familiar to you if you have solved the Pacific Atlantic Water Flow problem. Because they're similar in pattern. Although, this is a Dynamic Programming Question, so of course we need to have everything hyper optimised. Meaning, we're going to have a Memoization technique in order to prevent unnecessary calculations (Depth First Search in our case).
What we have been asked is to find the longest increasing path in a matrix. Which is a Graph Problem. Where the bi directional edges are the edges in the matrix. Up, down, left and right. We need to find that longest path. Which we ultimately want to find by Depth First Search.
Recommended Knowledge
- Graph Theory
- Depth First Search (Recursive)
- Memoization
- Matrix (Cache)
- Hash Map
- Topological Sort
What do we know?
- We're given a matrix that is m x n.
- This matrix represents a graph.
- We gotta find the longest path in this graph.
How we're going to do it:
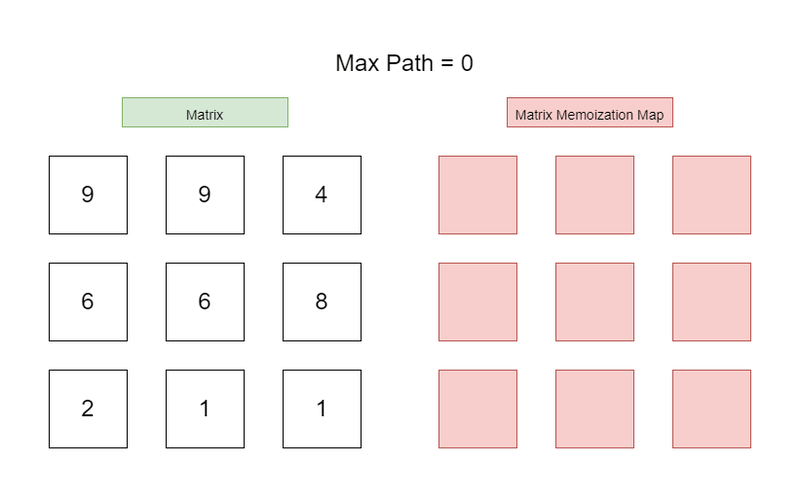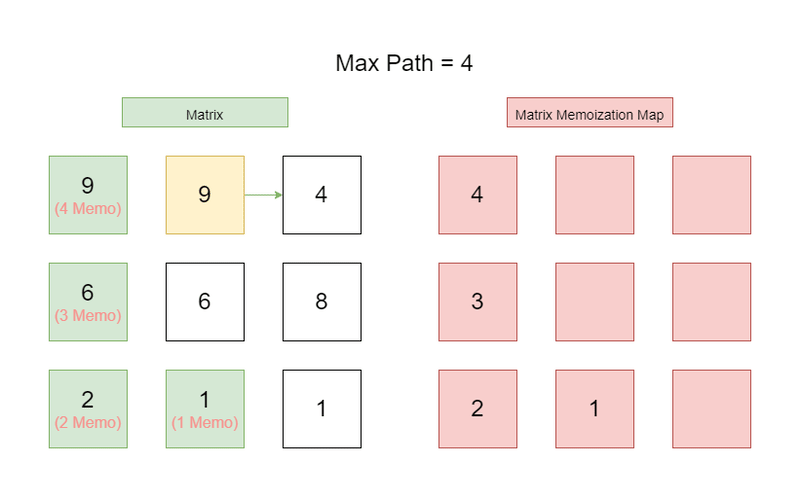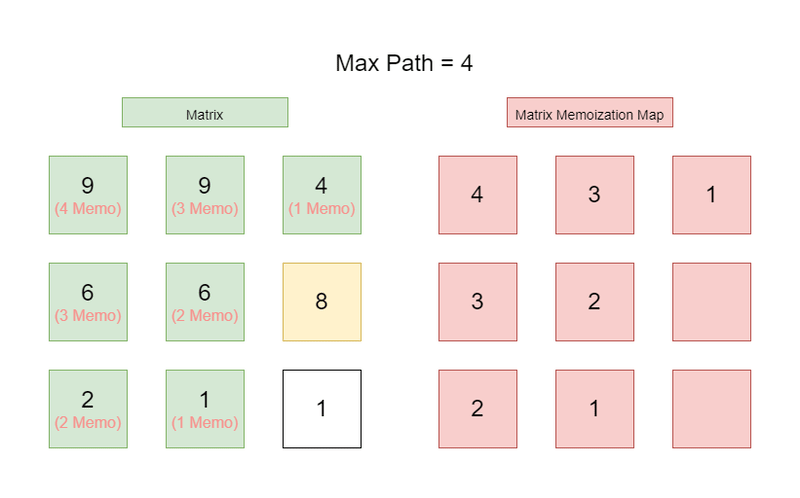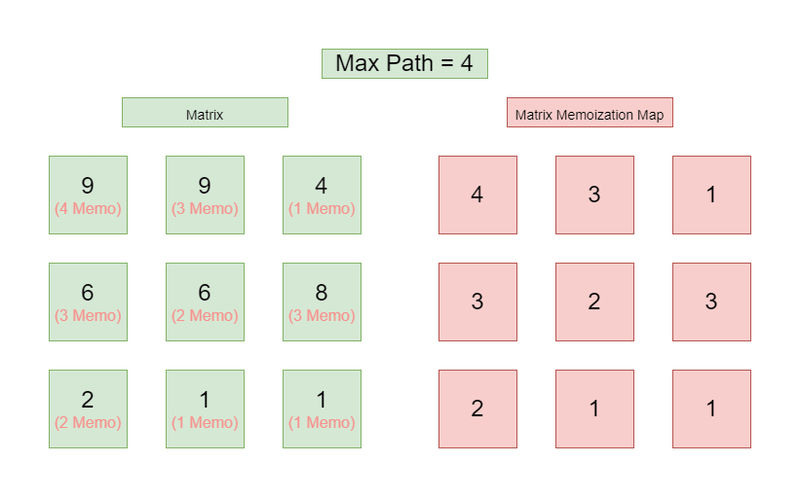
We're going to use Depth First Search to find the longest path. At each node within the matrix / graph, we will perform a Depth First Search to see if we're able to find a longer path. We do this recursively, until we have found the longest possible path from the root node we started from. Here, we use Topological Sort to backtrack to the root node, along the way create a Memoization cache of the longest possible path from that given node. We do this for every node in the graph. By the end, we know the longest path.
Wow, what a mouthful. In other words, we use DFS on each node to see how far we can get from that given node. We take this number and see if it's longer than the current longest path. If it is, we update the longest path. We then create a cache of the longest path from that node, so we don't have to redundantly calculate it later on.
Still don't understand, check the graphic at the top of the page. It's rather confusing all of this, Dynamic Programming is never simple. You need to know a ton of concepts before attempting Dynamic Programming.
- We're going to firstly create a
max_path_lengthvariable to store the longest path. - We're then going to create a
max_path_length_cachevariable to store the longest path from each node. Essentially, it's a mirror of the matrix where instead of the matrix values it's the longest path from that node. - We then go over each node in the matrix.
- We perform Depth First Search on all of them.
- During the Depth First Search, we ask if we're even allowed to travel to that node.
- If we're allowed to travel to that node, we then ask if we have already visited this node before. By asking the
max_path_length_cachevariable to see if it's already been visited. If it has, we get the value from the cache. If it hasn't, we perform a Depth First Search on that node too. - Once we have fully exhausted the Depth First Search, we then update the
max_path_lengthvariable if we have a longer path. This is done as apart of the Topological Sort algorithm. Which is confusing words for, 'Back tracking' which is also confusing words for 'Once I've done all the possible paths for this node I will do something.'
Big O Notation:
- Time Complexity: O(V + E) / O(n) | Where n is the number of nodes in the Matrix. V is the number of vertices in the graph. E is the number of edges in the graph as we're going to visit each vertex and each edge once. This is often represented as just O(n) as it's the number of nodes in the graph. If we didn't use the
max_path_length_cachevariable, we would have achieved a O((V + E) ^ 2) time complexity due to the repeated work. - Space Complexity: O(n) | Where n is the number of nodes in the
matrixgraph as we will be using a hashmap to keep track of all the nodes we've already visited.
Leetcode Results:
The Solution
/**
* @param {number[][]} matrix
* @return {number}
*/
var longestIncreasingPath = function (matrix) {
// So this is a really interesting question.
// It combines Dynamic Programming, Backtracking, Memoization,
// and Graph Theory
// The Basic premise of this solution is to perform DFS on each
// node, and keep track of the longest path, caching the results
// along the way. It sounds simple, and it is, but the initial development of this
// solution was far far from it.
// What we're going to do is reverse the logic, instead of going up nodes greater than
// us, we're only going to do it downwards. Why? Well, larger numbers are going to cover a greater
// area so it populates our cache faster, requiring less stack frames to traverse.
// Our Return Value.
let max_path_length = 0;
// Basic Maxes of the Matrix. Bound checks
const max_rows = matrix.length - 1;
const max_cols = matrix[0].length - 1;
// Our Memoization Array.
// Our Cache, that looks like `node => nodes_max_path_from_here`
// What this mean's is we don't need to check the same node twice.
const max_path_length_cache = new Map();
// Our Backtracking Function. We will be using Depth First Search
// to traverse the matrix / graph in 4 directions. Asking, "Can I go here?"
const depth_first_search = (row_index, col_index, prev) => {
// Is it within bounds?
// Meaning, can we travel to this location.
if (row_index > max_rows || col_index > max_cols || row_index < 0 || col_index < 0) {
return 0;
}
// Our Nodes Current value.
const node_val = matrix[row_index][col_index];
// Is this node greater than the previous node?
// Nope, we only want to waterfall down the graph's values. Throw it out.
if (node_val >= prev) {
return 0;
}
// Have we already explored this node and cached the result?
// If so, just return the cached result. If not, we'll need to explore it.
// and then cache the results from there.
if (!max_path_length_cache.has(`${row_index},${col_index}`)) {
// Explore the node's edges
const top = depth_first_search(row_index - 1, col_index, node_val); // UP
const bottom = depth_first_search(row_index + 1, col_index, node_val); // DOWN
const left = depth_first_search(row_index, col_index - 1, node_val); // LEFT
const right = depth_first_search(row_index, col_index + 1, node_val); // RIGHT
// Max Path Sum of this node
const nodes_max_path_value = Math.max(left, right, top, bottom) + 1;
// Cache the results,. We'll need to use this later.
max_path_length_cache.set(`${row_index},${col_index}`, nodes_max_path_value);
}
// Get the cached result.
return max_path_length_cache.get(`${row_index},${col_index}`);
};
// Traverse the matrix.
matrix.forEach((row, row_index) => {
row.forEach((col, col_index) => {
max_path_length = Math.max(depth_first_search(row_index, col_index, Infinity), max_path_length);
});
});
return max_path_length;
};




Top comments (0)