PROBLEM STATEMENT:
A factory has n machines which can be used to make products. Your goal is to make a total of t products.
For each machine, you know the number of seconds it needs to make a single product. The machines can work simultaneously, and you can freely decide their schedule.
Find the shortest time to make t products.
APPROACH:
Let's assume that all the products are made by the maximum element present in the array, i.e., by the machine which takes the maximum amount of time just to make a single product.
Then use a binary search to calculate the correct time.
Consider an example, 2,3,5.
Assume all the products are made by 3rd machine having time 5 units. So, the total time would be 5*(number of products).
Here, we are using basic mathematics. One machine takes x unit of time to make a single product, then, in y unit of time, it will make y/x product.
We are going to use the same approach in a binary search.
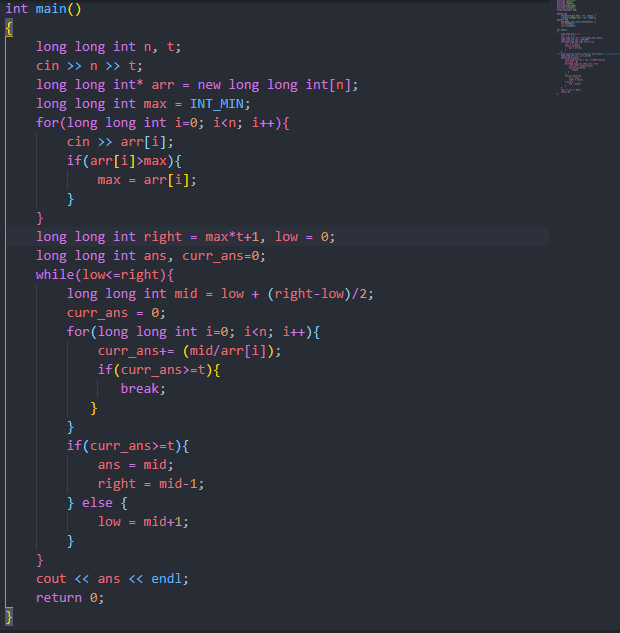
BINARY SEARCH IMPLEMENTATION LOGIC:
STEP 1: Take two pointers, low and high. Set low = 0 and high = *max_element*total + 1.
STEP 2: Create a while loop with a condition where low<=high.
Find mid-value of range low to high.
STEP 3: Calculate the number of products that can be made in "MID" time.
STEP 4: Compare this and with the target value, if it is greater than the target, it means, we can reduce our time to some more extent, so decrement high = mid-1 and store the current answer in a variable, else if it is lower than the target, which means, we have to increase our time more, so increment low = mid+1.
STEP 5: Output the final answer.
CODE IMPLEMENTATION
HAPPY CODING :)






Top comments (0)