Today we will be looking at how we can make use of commands and args in Docker to run our own processes when we spin up containers. This could be useful if you want to run one-off tasks without having to create your own images.
Let’s imagine that we want run a bash command. What’s the easiest way to do this? Just by spinning up a container using a lightweight image like busybox, ubuntu, debian? For instance, let’s say we use Debian as our base image.
docker run debian echo hello
We will get back “hello”, which is expected. What would happen if we check if the container is running?
The container has stopped running. Containers are not meant to host an operating system compared to a VM. When you run a basic container like Debian or Ubuntu, it will exit once you perform a docker run debian
However, in cases like Nginx, or Redis they will keep running unless you shut it down or it crashes for some reason. How does this happen?
Under the hood
Let’s have a look at their Dockerfiles. Note that these are oversimplified versions of these files (except for Debian).
Each of these files defines a CMD instruction at the bottom which tells them to run some command. In the case of Debian, it issues just bash which is just a shell, not a process. If you already spotted, both Redis and nginx Dockerfiles have definitions to spin up their processes - the Redis server and Nginx web server, respectively.
The CMD instruction
You would be wondering how would one go about customising which commands to run when you spin up a container. One way to specify commands when you start a container is by issuing the name of the executable when we run the container. For example,
docker run debian echo hello-world
If you check the container status, you will see that your container has stopped. Can we make this permanent? Yes, that’s why we need to have a Dockerfile to specify what’s our desired state when the container runs.
Say we use the CMD instruction in our Dockerfile, there are 3 ways to specify this according to Docker docs.
-
CMD ["executable","param1","param2"](exec form, this is the preferred form) -
CMD ["param1","param2"](as default parameters to ENTRYPOINT) -
CMD command param1 param2(shell form)
💡 There can only be one CMD instruction in a Dockerfile. If you list more than one CMD then only the last CMD will take effect.
FROM debian
CMD ["printf", "Hello from Test1"]
How can we dynamically define what gets printed? One caveat here is that if we are to pass in command line args it will not get appended to the existing CMD instruction we have set. Docker will try to execute as a command and our CMD instruction will get replaced. Let’s give this a test.
If you run docker run test1 hello, it will result in a “starting container process caused: exec: “hello”: executable file not found in $PATH: unknown.” error.
We can still pass in a command like so: docker run test1 printf hello but that beats the purpose of having a Dockerfile in the first place.
The ENTRYPOINT instruction
How can we specify something to run always so that we only need to specify its arguments. Let’s create another file called Test2.Dockerfile.
FROM debian
ENTRYPOINT ["printf", "Hello from %s\n"]
CMD ["Test2"]
The ENTRYPOINT instruction says Docker that whatever we have specified there, must be run when the container starts. In other words, if we are to pass in arguments, they will get appended to what we have specified there as the ENTRYPOINT.
docker build -t test -f Test2.Dockerfile .
If we run this now, we get the following.
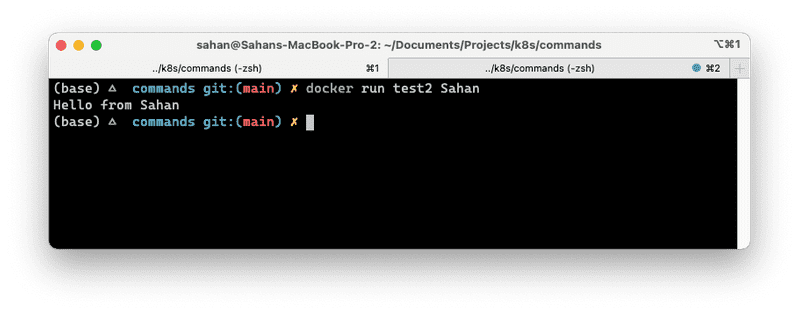
Cool! If we pass in a parameter now, it gets picked up and replaces the CMD instruction we had at line no. 3; but it will still show the output as we have defined in our ENTRYPOINT. This makes sense since there can be only one CMD instruction per container.
You would be thinking what’s the purpose of having CMD if it gets replaced? It’s really handy when you want to specify a default value.
What would happen if we specify multiple arguments?
What happend here? Let me know in the comments below what are your thoughts on this 😊
Conclusion
In this article we looked at passing in commands and args to container when we spin them up. In the next article, we will compare this to a Kubernetes Pod definition and figure out how we can do the same.








Top comments (1)
Nice 😄,
In the case of Debian, it issues just bash which is just a shell, not a process.But shell it self is some kind of application so it is a process isn't ?When you passed multiple arguments, inside a single container, it printed in new line because of Escape sequence
\n. Correct ?We are using
debianOS to print message to screen , cant we use the container default Command line itself to print ? Do containers have it ?