Preface
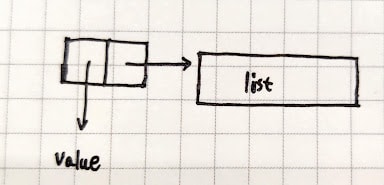
There is an interesting data structure in lisp, Cons, which uses function closures to encapsulate a two-tuple data structure and build any other data structure needed on top of it. Before this, although I knew about closures and other concepts and had written some higher-order functions, I had not thought that I could use functions to build data structures, and I will explain how to do that in ts below.
The basic definition is as follows
$$
c=cons(a,b)\\
car(c)=a\\
cdr(c)=b
$$
Initial Implementation
The cons initial implementation is simple and can be implemented in just a few lines of code. As you can see, it simply uses closures to bind the arguments a and b and return them when the function is executed.
function cons(a: number, b: number): (n: number) => number {
return (n: number) => (n === 0 ? a : b)
}
function car(cons: (n: number) => number) {
return cons(0)
}
function cdr(cons: (n: number) => number) {
return cons(1)
}
It can be used in the following way
const n = cons(1, 2)
console.log(car(n)) // 1
console.log(cdr(n)) // 2
To make it look a little more practical, first supplement its type with a generic type
export interface Cons<A, B> {
(s: 0): A
(s: 1): B
_0: A
_1: B
}
export function cons<A, B>(a: A, b: B): Cons<A, B> {
return ((s: 0 | 1) => (s === 0 ? a : b)) as any
}
export function car<T extends Cons<any, any>>(cons: T): T['_0'] {
return cons(0)
}
export function cdr<T extends Cons<any, any>>(cons: T): T['_1'] {
return cons(1)
}
Verify it with the following unit test
it('cons', () => {
const c = cons('hello', 1)
expect(car(c) as string).toBe('hello')
expect(cdr(c) as number).toBe(1)
})
It doesn't look like much, but it will be used below (the simplest binary structure) to combine into more complex data structures like chained tables and trees.
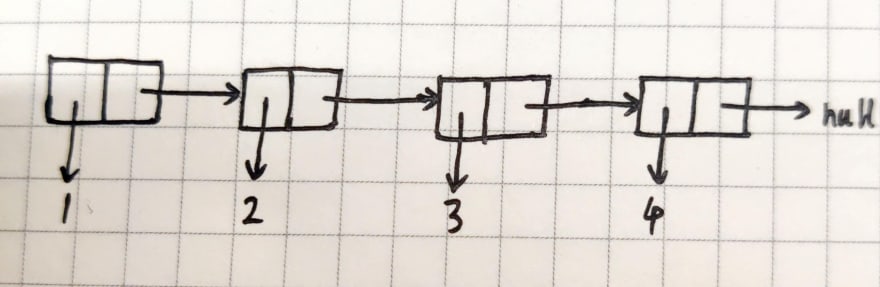
Chain Tables
In fact, once you have a binary, you can go on to combine any data structure you need, and a linked table is a simple example of this.
Here the car part of cons stores the value of the current node in the chain table, and cdr stores a pointer to the next node.
type List<T> = Cons<T, List<T>> | null
function list(): null
function list<T>(.. .args: T[]): Exclude<List<T>, null>
function list<T>(... .args: T[]): List<T> {
function iter(i: number): List<T> {
return i === args.length ? null : cons(args[i], iter(i + 1))
}
return iter(0)
}
Here is a chain table storing 4 elements
list(1, 2, 3, 4)
It will be a cons nested call procedure
cons(1, cons(2, cons(3, cons(4, null))))
You can write map/filter/reduce functions for it
map/filter is nothing complicated, just recursive processing of each node
function map<T, R>(list: List<T>, f: (i: T) => R): List<R> {
return list === null ? null : (cons(f(car(list)), map(cdr(list)!, f)) as any)
}
function filter<T>(list: List<T>, f: (i: T) => boolean): List<T> {
return list === null
? null
: f(car(list))
? cons(car(list), filter(cdr(list), f))
: filter(cdr(list), f)
}
The following diagram uses map processing
reduce is a little special in that it is an iterative recursion
function reduce<T>(list: List<T>, f: (res: T, v: T, i: number) => T): T
function reduce<T, R>(
list: List<T>,
f: (res: R, v: T, i: number) => R,
init: R,
): R
function reduce<T, R>(
list: List<T>,
f: (res: R, v: T, i: number) => R,
init?: R,
): R {
function iter(list: List<T>, init: R, i: number): R {
return list === null ? init : iter(cdr(list)!, f(init, car(list), i), i + 1)
}
return init! == undefined
? iter(list, init, 0)
: iter(cdr(list!), car(list!) as unknown as R, 1)
}
It can be used in the following way
const res = reduce(
map(
filter(list(1, 2, 3, 4), (i) => i % 2 === 0),
(i) => i * 2,
),
(a, b) => a + b,
0,
)
console.log(res) // 12
In theory, it should be easy to convert map/filter to a higher-order function based on reduce, for example the following code implements map/filter based on reduce in js
function map<T, R>(list: T[], f: (i: T) => R): R[] {
return list.reduce((res, i) => {
res.push(f(i))
return res
}, [] as R[])
}
function filter<T>(list: T[], f: (i: T) => boolean): T[] {
return list.reduce((res, i) => {
if (f(i)) {
res.push(i)
}
return res
}, [] as T[])
}
If one wishes to base the map/filter implementation of the linked table here on reduce, this is currently not possible. Note that the above code uses push, which is a modify operation and is more recommended for immutable state in functional programming. So, is there some way to do it even without changing the state? I will try to implement it.
function concat<T>(a: List<T>, b: List<T>): List<T> {
return a === null ? b : cons(car(a), concat(cdr(a), b))
}
function mapForReduce<T, R>(arr: List<T>, f: (i: T) => R): List<R> {
return reduce(arr, (res, i) => concat(res, list(f(i))), null as List<R>)
}
function filterForReduce<T>(arr: List<T>, f: (i: T) => boolean): List<T> {
return reduce(
arr,
(res, i) => (f(i) ? concat(res, list(i)) : res),
null as List<T>,
)
}
Of course, someone might say: Isn't it inefficient to concatenate two chains every time you iterate over an element? Yes, it is indeed very inefficient, so another slightly odd approach can be used.
function mapForReduce<T, R>(list: List<T>, f: (i: T) => R): List<R> {
return reduce(
list,
(res, i) => {
return i === null ? res : (next) => res(cons(f(i), next))
},
(r: List<R>) => r,
)(null)
}
function filterForReduce<T>(list: List<T>, f: (i: T) => boolean): List<T> {
return reduce(
list,
(res, i) => (f(i) ? (next) => res(cons(i, next)) : res),
(r: List<T>) => r,
)(null)
}
Admittedly, this approach doesn't seem to accumulate a stack on each recursion, but it also wraps the function res over and over, and eventually passing in a single argument to call it all at once when reduce ends doesn't solve the fundamental problem, so the following implementation of setCar/setCdr
Support for modifying car/cdr
To implement set, you actually have to modify the parameters of the closure binding.
export interface Cons<A, B> {
(s: 'car'): A
(s: 'cdr'): B
(s: 'setCar'): (v: A) => void
(s: 'setCdr'): (v: B) => void
_0: A
_1: B
}
export function cons<A, B>(a: A, b: B): Cons<A, B> {
return ((s: string) =>
s === 'car'
? a
: s === 'cdr'
? b
: s === 'setCar'
? (v: A) => (a = v)
: (v: B) => (b = v)) as any
}
export function car<T extends Cons<any, any>>(cons: T): T['_0'] {
return cons('car')
}
export function cdr<T extends Cons<any, any>>(cons: T): T['_1'] {
return cons('cdr')
}
export function setCar<T extends Cons<any, any>>(cons: T, v: T['_0']): void {
return cons('setCar')(v)
}
export function setCdr<T extends Cons<any, any>>(cons: T, v: T['_1']): void {
return cons('setCdr')(v)
}
This can be verified using the following unit test
it('cons', () => {
const c = cons('hello', 1)
expect(car(c) as string).toBe('hello')
expect(cdr(c) as number).toBe(1)
setCar(c, 'liuli')
setCdr(c, 2)
expect(car(c) as string).toBe('liuli')
expect(cdr(c) as number).toBe(2)
})
However, an alternative implementation is proposed in the course that uses a higher-order function implementation entirely, without using internal judgments in cons.
export interface Cons<A, B> {
(m: (a: A, b: B, setA: (a: A) => void, setB: (b: B) => void) => any): any
_0: A
_1: B
}
export function cons<A, B>(a: A, b: B): Cons<A, B> {
return ((
m: (a: A, b: B, setA: (a: A) => void, setB: (b: B) => void) => any,
) =>
m(
a,
b,
(n: A) => (a = n),
(n: B) => (b = n),
)) as any
}
export function car<T extends Cons<any, any>>(cons: T): T['_0'] {
return cons((a) => a)
}
export function cdr<T extends Cons<any, any>>(cons: T): T['_1'] {
return cons((_a, b) => b)
}
export function setCar<T extends Cons<any, any>>(
cons: T,
value: T['_0'],
): void {
cons((_a, _b, setA) => setA(value))
}
export function setCdr<T extends Cons<any, any>>(
cons: T,
value: T['_1'],
): void {
cons((_a, _b, _setA, setB) => setB(value))
}
Now, re-implement mapForReduce/filterForReduce
function mapForReduce<T, R>(list: List<T>, f: (i: T) => R): List<R> {
const init = cons(null, null) as unknown as List<R>
reduce(
list,
(curr, i) => {
const next = cons(f(i), null) as List<R>
setCdr(curr!, next)
return next
},
init,
)
return cdr(init!)
}
function filterForReduce<T>(list: List<T>, f: (i: T) => boolean): List<T> {
const init = cons(null, null) as unknown as List<T>
reduce(
list,
(curr, i) => {
if (!f(i)) {
return curr
}
const next = cons(i, null) as List<T>
setCdr(curr!, next)
return next
},
init,
)
return cdr(init!)
}
For the code mapForReduce(list(1, 2, 3, 4), i => i) the iterative process graph
| i | curr | init |
|---|---|---|
| 1 | (null, null) | (null, null) |
| 2 | (1, null) | (null, (1, null)) |
| 3 | (2, null) | (null, (1, (2, null))) |
| 4 | (3, null) | (null, (1, (2, (3, null)))) |
| return | (null, (1, (2, (3, (4, null))))) |
As you can see, each time you modify the previous node, and use cons to construct a new node with the current value as the next iteration, you end up traversing the entire list and making a copy of the entire list.
Trees
Since you can construct a chain table with cons, you can also construct a tree structure by defining a tree structure.
A node is composed of a value and possible children, so we define a tree node like this.
cons(value, list(sub1, sub2, ...subN))
The implementation is very simple
type Tree<T> = Cons<T, List<Tree<T>>>
function tree<T>(value: T, children: List<Tree<T>>> = null) {
return cons(value, children)
}
const t = tree(1, list(tree(2, list(tree(3)))), tree(4)))
expect(car(t)).toBe(1)
expect(car(car(cdr(t)!))) .toBe(2)
It is also possible to implement map/filter/reduce with a tree structure, and you can see that the line implementations are simple list-based map/filter implementations.
function treeReduce<T, R>(tree: Tree<T>, f: (r: R, v: T) => R, init: R): R {
init = f(init, car(tree))
map(cdr(tree), (i) => {
init = treeReduce(i, f, init)
})
return init
}
function treeMap<T, R>(tree: Tree<T>, f: (v: T) => R): Tree<R> {
return cons(
f(car(tree)),
map(cdr(tree)! , (i) => treeMap(i, f)),
)
}
function treeFilter<T>(tree: Tree<T>, f: (v: T) => boolean): Tree<T> | null {
if (!f(car(tree))) {
return null
}
return cons(
car(tree),
filter(
map(cdr(tree)! , (i) => treeFilter(i, f)! ,
(i) => i ! == null,
),
)
}
Test it
const t = tree(1, list(tree(2, list(tree(3)))), tree(4)))
it('basic', () => {
expect(car(t)).toBe(1)
expect(car(car(cdr(t)!))) .toBe(2)
})
it('treeReduce', () => {
expect(treeReduce(t, (r, i) => [. .r, i], [] as number[])).toEqual([
1, 2, 3, 4,
])
})
it('treeMap', () => {
expect(
treeReduce(
treeMap(t, (i) => i * 2),
(r, i) => [. .r, i],
[] as number[],
),
).toEqual([1, 2, 3, 4].map((i) => i * 2))
})
it('treeFilter', () => {
const res = treeFilter(t, (i) => i % 2 === 1)
expect(treeReduce(res!, (r, i) => [. .r, i], [] as number[])).toEqual([1])
})
Conclusion
lisp is a seemingly simple language, because it seems to be all about expressions, and it doesn't offer as many ways to construct complex data (like object objects, structs, classes, etc.) as modern languages. But as you can see here, it is possible to construct arbitrarily complex data structures by supporting the simplest complex data, and the building blocks of all complex data are so simple as to be unbelievable.
In fact, it is so easy to write a lisp toy parser and runtime using ts that I will demonstrate it later.




Top comments (0)