Disjoint Set Union (DSU)
Overview
The Disjoint-set data structure allows us to very quickly determine if two items are in the same set (or equivalently determine if two vertices are in the same connected component), and also to very quickly unite two sets (or equivalently combine two connected components into one connected component).
Interface
initSet(N)* Initializes an element and sets it to be its own set
unionSet(i,j)* Takes two elemements and combines them in one set
findSet(i)* Find the set an element belongs to
isSameSet(i,j) Find if two elements belong to the same set
numDisjointSets Find number of sets (connected componants)
sizeOfSet Find the size of a set an element belongs to
Data Structure
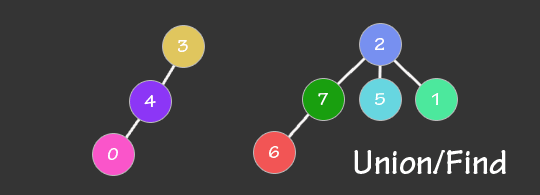
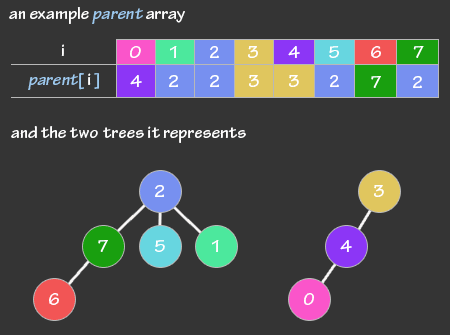
In its simplest form the DSU is an array of integers called parent where every ith item has its parent stored in the parent[i] or the array, These relationships create one, or more, virtual trees.
There you can see that 6 is under 7 in the tree, because parent[6] = 7. Also note that 2 and 3 have no parents, because parent[2] = 2 and parent[3] = 3.
Each tree is a disjoint set. If two elements are in the same tree, then they are in the same disjoint set. The root node (or the topmost node) of each tree is called the representative of the set. There is always a single unique representative of each set. As you can see, if i is the representative of a set, then parent[i] = i. If i is not the representative of his set, then it can be found by traveling up the tree until we find the representative.
Simple (Naive) implementation
We can already write a simple implementation of a DSU. It will be inefficient, but then we'll improve it with two techniques, resulting in an almost constant time of work.
The three main functions of the dsu are:
initSet(N) Initially each element belongs to its own set so we set it to be its own parent.
findSet(v)A simple recursive functions that climbs the parents of an element till it reaches the root of the set it belongs to.
unionSet(a,b)To combine two sets we firstly need to find if they belong to the same set (already unioned). If not then we assign them to the same set by setting the parents of j to be i.
vector < int > parent;
void initSet(int N)
{
parent.assign(N, 0);
for (int i = 0; i < N; i++)
parent[i] = i;
}
int findSet(int i)
{
if (i == parent[i])
return i;
return findSet(parent[i]);
}
void unionSet(int i, int j)
{
i = findSet(i);
j = findSet(j);
if (i != j)
parent[j] = i;
}
However, such implementation is considered to be inefficient as building a large tree will cause the depth of the different chains to be larger which will cause a worst case of O(n) for the findSet function
Efficient Implementation
To build a more efficient DSU there are two optimizations that can be done Path Compression and Combine by Rank.
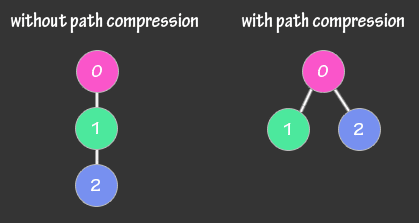
Path Compression
Normally when using findSet to find a set of an element, the recursive function will traverse the whole parent chain of this element untill it reaches the representative or the effective parent of this set, This will cause the complexity of such operation to be of O(n) to avoid that we don't want to store the immediate ancestor for the element but store the top ancestor instead.
The new findSet() after applying the path compression concept should be as follows, notice that instead of returning the found parent, we save it before doing so.
The complexity after applying the path compression concept only would be O(log n) provided that unionSet() calls findSet() twice and does other O(1) operations that are ignored in the complexity calculation so the proof is concentrated on the O(log n) of findSet().
int findSet (int i) {
if (i == parent[i])
return i;
return parent[i] = findSet (parent[i]);
}
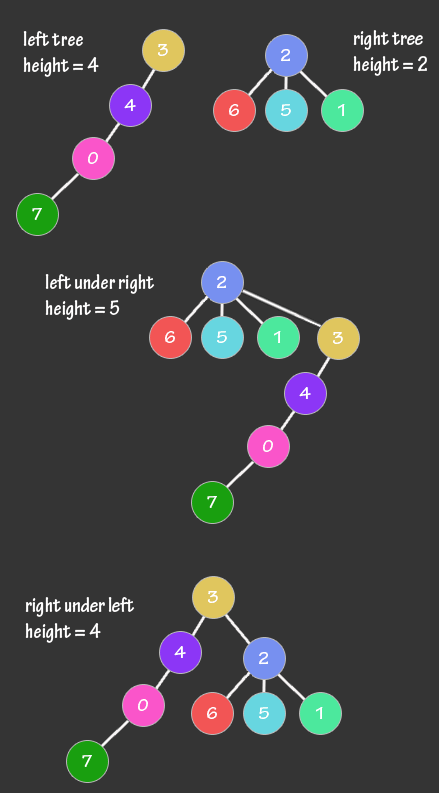
Union by Rank
The previous improvement changed the findSet() operation to make the heights of the trees smaller. This improvement, called Union by Rank, changes the unionSet() operation to also make the heights of the trees smaller. The basic idea is that when joining two sets, the shorter set becomes the child of the longer one which will cause the height of the tree to be smaller.
This technique has two variants, one that ranks the trees based on tree size (number of vertices) and the other one is based on tree depth. In this example we will be implementing the tree depth union by rank variant.
To Acheive this a rank for each node is initially set to zero and then incremented every time a new node is added to it.
The complexity by using only the Union by Rank technique will effectivly be reduced to O(log n)
vector < int > parent;
vector < int > rank;
void initSet(int N)
{
rank.assign(N, 0); //Rank is now initialized
parent.assign(N, 0);
for (int i = 0; i < N; i++)
parent[i] = i;
}
void unionSet(int i, int j)
{
i = findSet(i);
j = findSet(j);
if (i != j)
{
int x = findSet(i), y = findSet(j);
if (rank[x] > rank[y])
parent[y] = x;
else
{
parent[x] = y;
if (rank[x] == rank[y])
rank[y]++; //Rank update
}
}
}
Complexity after improvements
The complexity of the DSU after adding either one of Path Compression or Union by Rank acheives an avarage of O(log n)
On combining both techniques together the complexity will achieve a near constant time O(1)
Putting it all together
The full class after applying Path Compression and Union by Rank. Also notice that three operations have been added
isSameSet(i,j) Find if two elements belong to the same set
numDisjointSets Find number of sets (connected componants)
sizeOfSet Find the size of a set an element belongs to
class UnionFind //OOP Style class
{
private:
vector <int>p, rank, setSize;
int numSets;
public:
UnionFind(int N)
{
setSize.assign(N, 1);
numSets = N;
rank.assign(N, 0);
p.assign(N, 0);
for (int i = 0; i < N; i++)
p[i] = i;
}
int findSet(int i) { return (p[i] == i) ? i : (p[i] = findSet(p[i])); }
bool isSameSet(int i, int j) { return findSet(i) == findSet(j); }
void unionSet(int i, int j)
{
if (!isSameSet(i, j))
{
numSets--;
int x = findSet(i), y = findSet(j);
if (rank[x] > rank[y])
{
p[y] = x;
setSize[x] += setSize[y];
}
else
{
p[x] = y;
setSize[y] += setSize[x];
if (rank[x] == rank[y])
rank[y]++;
}
}
}
int numDisjointSets() { return numSets; }
int sizeOfSet(int i) { return setSize[findSet(i)]; }
};</int>
Some Applications of DSU
- Dynamically finding connected components in a graph
- Searching for connected components in an image
- Finding distances between a vertex and a representative of its set
- Finding LCA in a tree






Top comments (0)