Binary search and big O notation

In this article, I will teach you about big O notation and we will also implement binary search in Python3.

Big O notation

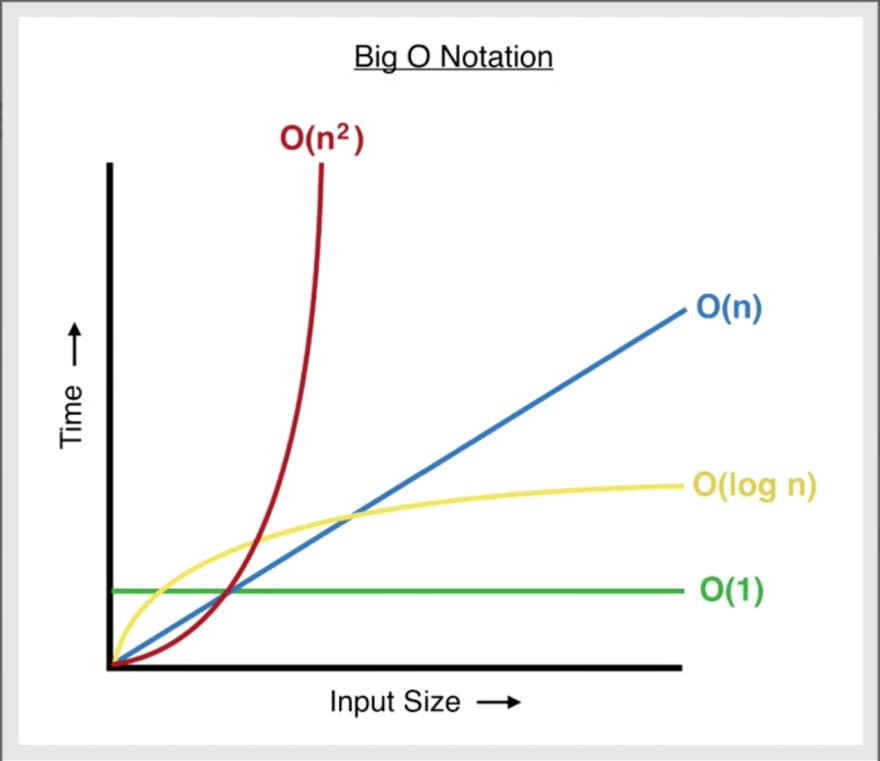
Big O notation is a special notation that tells you how fast your algorithm is. Why does big O notation matter? When you use people's algorithms, it's nice to understand how fast or slow they are. When it comes to measuring algorithms it's not enough to measure the time in seconds because when an algorithm is working with small amounts of operations it can be hard to see a difference. But the more operations you will need to compute, the more time will scale. With big O notation, you can quickly see how much the algorithm will scale based on input. The amount of input into the algorithm is called n.

For example, O(n) will scale linearly while O(n^2) will scale exponentially.

Some common big O notations you will see are the following:

• O(1) static.
• O(log n), also known as log time. Example: Binary search.
• O(n), also known as linear time. Example: Simple search.
• O(n * log n). Example: A fast sorting algorithm.
• O(n^2). Example: A slow sorting algorithm.
• O(n!). Example: A super slow algorithm, like the traveling salesperson problem.

Binary Search

When you need to search for something you'll probably use some kind of algorithm. One popular algorithm is binary search. One of the reasons because it's so popular is its efficiency(O(log n)). Now how does binary search work?

Imagine a sorted list of numbers.
[1, 4, 6, 7, 9, 21, 43]
If I would like to see if number 6 is inside this list and where it is located I could go through each element in the list until I find the number 6. That's simple search. The problem with simple search is that with large lists it will be slow. If I would instead use binary search we could search the list fast even with a large list.

How binary search starts is as the following. Start looking at the number seven. If the number we are looking for is lower we move forward and only look at the left side of the list. If it's higher we only look on the right side. In this case, 6 is lower than 7 so we will look at the left side. Now the numbers we care about are these.
[1, 4, 6]

Now we do the same thing we did before. We start to look at 4, is 6 higher or lower? Higher. We therefore move forward and our list only looks like this:
[6]

Now when we do the same thing again, we'll see that the item we are looking at is the number we are searching for. Boom, we found it! Now if instead, the number we were looking for was 5, we would not have found anything, then our program would return -1 instead.

To sum it up

1. Look at the item in the middle(lowest value:highest value) of the list
2. If the list is empty return -1
3. Check if the item is the one you're looking for.
4. If yes return index
5. Check if the item is lower or higher than what you're looking for
6. Modify list/lowest and highest value
7. Start over

Now let's implement this in code

Binary search in Python 3

def bin_search(item, arr):
    low, high = 0, len(arr) - 1

    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == item:
            return mid

        if arr[mid] < item:
            low = mid + 1
        elif arr[mid] > item:
            high = mid - 1
     return -1

my_list= [1, 4, 6, 7, 9, 21, 43]

print(bin_search(6, my_list)) // Returns 2
print(bin_search(5, my_list)) // Returns -1

The code above is a simple implementation of binary search, there are different ways to implement a binary search and this is one of them. This program will go through the list to search for the item we are looking for.

Recap

• Algorithms speed is not measured in seconds.
• Algorithm times are written in big O notation.
• Big O notation is showing in terms of the growth of an algorithm.
• Some common Big O notations: O(n), O(log n), O(n^2), O(n * log n)
• Binary search is a fast searching algorithm. Much faster than simple search.

Thank you for reading this short post about Big O notation and Binary Search. This post is part of a data structures and algorithms series I'm working on so make sure to leave a follow if you're interested to see more.