Fly Straight, Dammit!

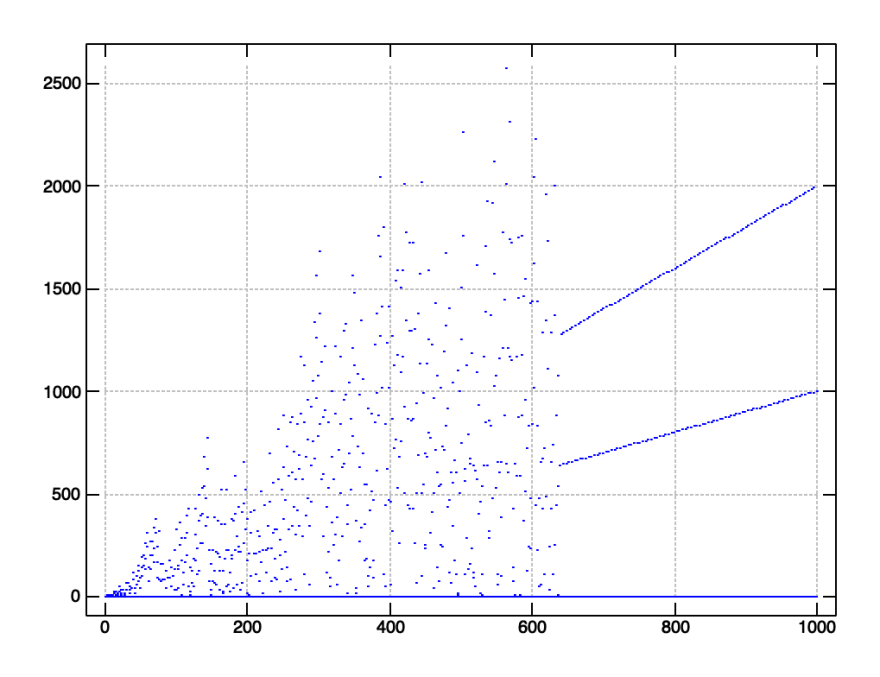
Numberphile recently posted a video about an interesting recursive function called “Fly Straight, Dammit!” which, when plotted, initially seems chaotic, but after six hundred thirty eight iterations, instantly stabilizes.

This sounds like a perfect opportunity to flex our J muscles and plot this function ourselves!

An Imperative Solution

The simplest approach to plotting our “Fly Straight, Dammit!” graph using the J programming language is to approach things imperatively:

a =: monad define
  if. y < 2 do.
    1
  else.
    py =. a y - 1
    gcd =. y +. py
    if. 1 = gcd do.
      1 + y + py
    else.
      py % gcd
    end.
  end.
)

We’ve defined our a monadic verb to return 1 if we pass in a “base case” value of 0 or 1. Otherwise, we recursively execute a on y - 1 to get our py, or “previous y”. Next, we check if the gcd of y and py equals 1. If it does, we return 1 + y + py. Otherwise, we return py divided by gcd.

This kind of solution shouldn’t look too foreign to anyone.

Let’s plot values of a to verify our solution:

require 'plot'
'type dot' plot a"0 i. 1000

This works, but it’s very slow. We know that our recursive calls are doing a lot of duplicated work. If we could memoize the results of our calls to a, we could save quite a bit of time. Thankfully, memoizing a verb in J is as simple as adding M. to the verb’s declaration:

a =: monad define M.
  ...
)

Now our imperative solution is much faster.

Using Forks and Hooks

While our initial solution works and is fast, it’s not taking advantage of what makes J a unique and interesting language. Let’s try to change that.

The meat of our solution is computing values in two cases. In the case when y and py have a greatest common divisor equal to 1, we’re computing 1 plus y plus py. Our imperative, right to left implementation of this computation looks like this:

1 + y + py

We could also write this as a “monadic noun fork” that basically reads as “1 plus the result of x plus y:

a_a =: 1 + +

Similarly, when we encounter the case where the greatest common divisor between y and py is greater than 1, we want to compute py divided by that gcd. This can be written as a “dyadic fork”:

a_b =: [ % +.

We can read this fork as “x divided by the greatest common divisor of x and y.”

Now that we’ve written our two computations as tacit verbs, we can use the “agenda” verb (@.) to decide which one to use based on the current situation:

a_a =: 1 + +
a_b =: [ % +.

a =: monad define M.
  if. y < 2 do.
    1
  else.
    py =. a y - 1
    has_gcd =. 1 = y +. py
    py (a_b ` a_a @. has_gcd) y
  end.
)

If has_gcd is 0, or “false”, we’ll return the result of py a_b y. Otherwise, if has_gcd is 1, we’ll return the result of py a_a y.

More Agenda

We can elaborate on the idea of using agenda to conditionally pick the verb we want to apply to help simplify out base case check.

        <p>I find myself producing lots of ranging content from books and articles, like the one you're reading now, to open source software projects. If you like what I'm doing, <strong>nothing shows your support more than signing up for <a href="#newsletter">my mailing list</a></strong>.</p>

First, let’s define our base case and recursive case as verbs that we can combine into a gerund. Our base case is simple. We just want to return 1:

base_case =: 1:

Our recursive case is just the (memoized) else block from our previous example:

recursive_case =: monad define M.
  py =. a y - 1
  has_gcd =. 1 = y +. py
  py (a_b ` a_a @. has_gcd) y
)

Our function, a wants to conditionally apply either base_case or recursive_case, depending on whether y is greater or less than one. We can write that using agenda like so:

a =: base_case ` recursive_case @. (1&<)

And because our base_case verb is so simple, we can just inline it to clean things up:

a_a =: 1 + +
a_b =: [ % +.

recursive_case =: monad define M.
  py =. a y - 1
  has_gcd =. 1 = y +. py
  py (a_b ` a_a @. has_gcd) y
)

a =: 1: ` recursive_case @. (1&<)

Using agenda to build conditionals and pseudo-“case statements” can be a powerful tool for incorporating conditionals into J programs.

Going Further

It’s conceivable that you might want to implement a tacit version of our recursive_case. Unfortunately, my J-fu isn’t strong enough to tackle that and come up with a sane solution.

That said, Raul Miller came up with a one-line solution (on his phone) and posted it on Twitter. Raul’s J-fu is strong.