It’s much easier to multiply numbers together than to factor them apart. That’s the basics of RSA encryption.
In particular, the RSA encryption works with two large primes p and q, is quickly and easy to find the product pq but it is harder to recover the factors p and q from n. Generally p and q are numbers with hundreds of digits, factoring a number of this magnitude is very slow.
The algorithm
To encode the message we need n = pq and a positive integer e that
be reversible module φ (n). We talk about the Euler’s totient function before.
We will call the encoding key pair (n, e) of the RSA system. We will encode each message block separately and the final message will be the coded blocks sequence.
Important: Blocks already encoded can not be assembled to form a new number. This should make decoding impossible, as we’ll see later!
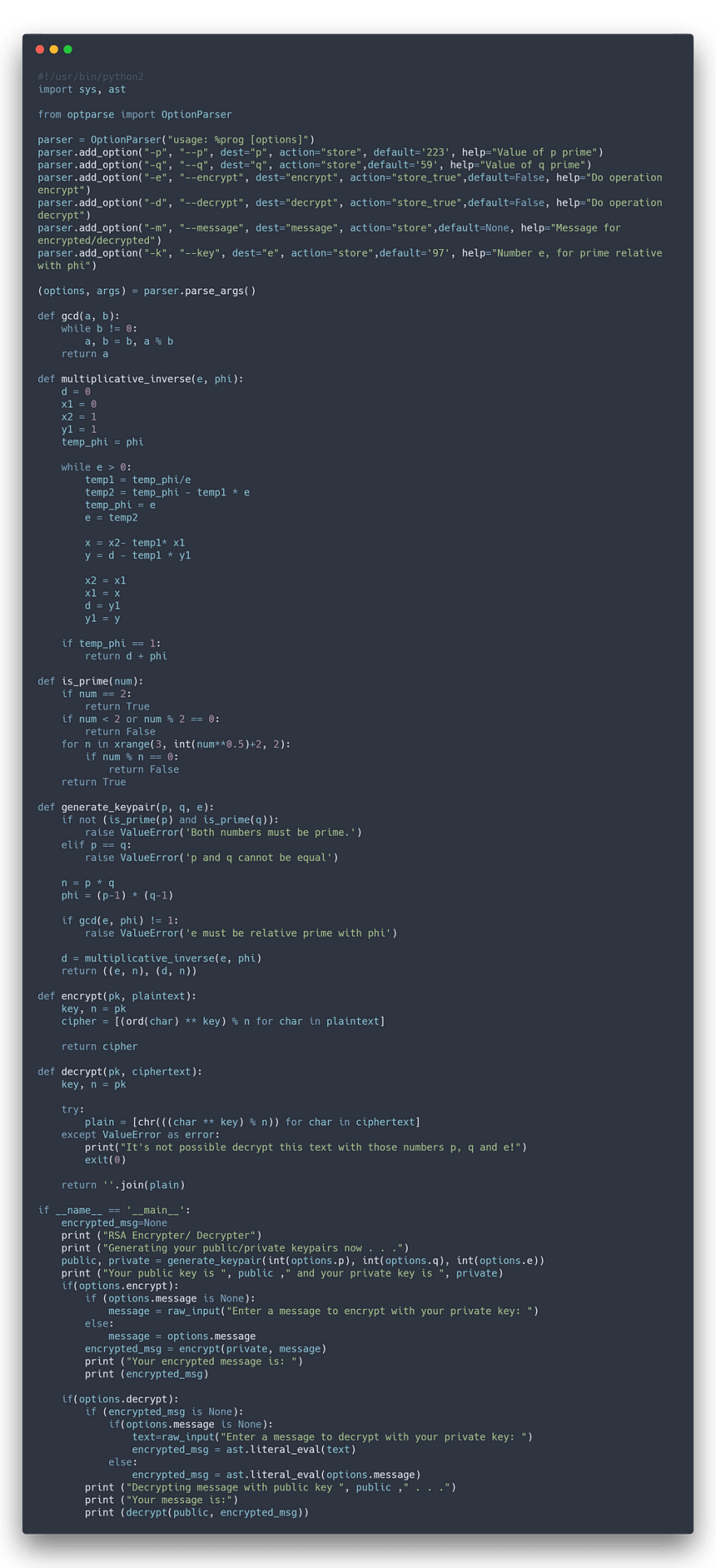
Let’s now show how to encode each block b. We will call the coded block of C(b). First, remember that b is an integer smaller than n. We calculate C(b) as follows:
where 0≤C (b) <n.
Let’s see how to decode a block of the encoded message. The information we need to be able to decode consists of two numbers: n and the inverse of e module φ(n), which we denote d. We will call the pair (n, d) of decode key. Be the one block of the message encoded. Then D(a) will be the result of the decoding process. The way to calculate D(a) is:
where 0 ≤ D (a) <n.
First, it is very easy to calculate d, if we have φ(n) and e : simply apply the extended Euclidean algorithm. On the other hand, it is clear that if b is a block of the original message, then we expect D(C(b)) = b, otherwise we will not have a useful code.
Finally, since the beginning of the notes we have been insisting that we encode using n and decode using p and q; so you need to factor n to decode. At this point we see that is not strictly true. In addition to the n itself, we only need to know the inverse d of e modulo φ(n) to decode. It turns out that we only know how to calculate d by applying the extended algorithm to e and φ(n).
Proof that RSA works
The obvious question which now arises is: D(C(b)) = b?
That is, by decoding a coded message block, can we find a block of the original message? Because otherwise all our effort was meaningless …
Consider then n = pq. We will prove that D(C(b)) ≡ b mod (n).
How 1≤ b, D (C (b)) ≤ n-1.
By definition, we have:
But d is the inverse of e module φ(n). Then there is an integer k such that ed=1 + kφ (n).
Soon,
If b and n are relatives primes, then we can use Euler’s Theorem:
Suppose that b and n are not prime to each other. Since n = pq, p and q are distinct primes, then φ(n) = (p-1)(q-1).
Soon,
If b and p are relative prime, then we can use Fermat’s Theorem, and we have bᵖ⁻¹ ≡ 1 mod (p).
Therefore, bᵉᵈ ≡ b mod (p), whichever is b.
We do the same for prime q, we get, bᵉᵈ ≡ b mod (q).
Therefore,
as we wanted.
Implementation
As an developer I have a necessary to put code in everywhere, even when don’t need it, so I will put here a simple implementation of this algorithm, and that can be useful later





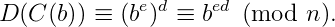

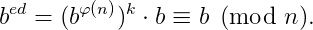
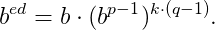


Top comments (0)