Classical puzzle for every junior developer is to find n in the fibonacci sequence. To be specific, it is a sequence where a number is the sum of the two preceding ones, starting from 0 and 1. So if you need to find 7-th element in sequence, the answer is 13.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34
Let's solve this exercise using 3 popular movies with Keanu Reeves.
The Day the Earth Stood Still
In most cases interviewer want to see your understanding of recursion. This is one of the first headaches of novice developers (second is C pointers I guess).
The most simple expected solution is here:
def fib(n)
return n if n <= 1
fib(n - 1) + fib(n - 2)
end
fib(7) #=> 13
This solution is not effective. The time taken by recursive Fibonacci is O(2^n) or exponential. For more details follow this beginner friendly Big O notation guide A Rubyist's Guide to Big-O Notation. In our solution we calculate all numbers in range 0..n again and again for every n in sequence. For big numbers (>80) the quanity of computation steps can be more than there are atoms in our universe! At this point it would freeze not only your computer, but all Earth computation resorces forefer.
Let's loot at our call stack. When you call fib(7), it recursevery calls fib(6) and fib(5). fib(6) cals fib(5) again with all calculations from the start.
Johnny Mnemonic
If you are more experienced developer, you would probably add memorization to reduce number of calculations. And in most cases interviewer will be happy with such solution.
module Fib
@memo = [0,1]
def self.calc(num)
return num if num < 2
@memo[num] ||= self.calc(num - 1) + self.calc(num - 2)
end
end
Fib.calc(7) #=> 13
Here we save every new number in sequence to @memo and do not calculate it again. What about complexity? It'll be O(n) where n is the number of numbers generated. Good enough.
The Matrix
But what if you want to impress your interviewer and provide O(log n) solution? Follow the White Rabbit!
require "matrix"
def fib(n)
(Matrix[[1,1],[1,0]] ** n)[1,0]
end
fib(7) #=> 13
A lot of math here! Relax, the key point is that you can simply raise [[1,1][1,0]] matrix to the power of n. And extract your answer from new matrix at [1,0] or [0,1].
You can show that you did not skip classes of higher mathematics in college and most likely impress the interviewer with your solution. But always remember that you may be required to explain your matrix solution. Therefore, arm yourself with a math book, because it is not always boring, but often very useful and fun!

![Cover image for How to impress employer at ruby technical interview with a help of Keanu Reeves [Fibonacci sequence]](https://media2.dev.to/dynamic/image/width=1000,height=420,fit=cover,gravity=auto,format=auto/https%3A%2F%2Fdev-to-uploads.s3.amazonaws.com%2Fi%2Fvr014wrl8iillytb3e24.png)

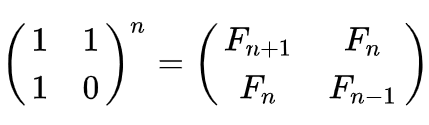





Top comments (0)