Justification and inspiration
I was originally inspired by the geohash coordinate system, proposed as an alternative to latitude-longitude coordinates for mapping the Earth’s surface, and by later proposals like plus codes. Tetracoordinates are not meant to compete with either of those proposals for use as geographical coordinates, and I hope that plus code or a derivative continues to improve and be more widely adopted for addressing and navigation.
The tetracoords system rather tries to address specific issues with the geohash approach while keeping many of the same advantages, focusing especially on use in software (as opposed to being human-readable).
For example, imagine you’re creating a 2D multiplayer game, where all objects and avatars need to have assigned positions. Using traditional 2D vectors, you then need to determine a scale and precision for that game space. If you use integers, then nothing can be at position 0.5,-0.5 because an integer doesn’t allow for precision at place value 10^-1. If you use floats, then the further something is from the origin 0,0, the less digits its position can allocate for determining precision, and vice versa. These limitations usually mean that the dimensions (and max zoom level) of the game space cannot grow over time.
Using a tetracoord-based datatype, however, you don’t need to specify scale or precision beforehand, and different tetracoords with different numbers of significant digits (of different sizes in memory) can be used for different contexts as needed (a fast airplane has high scale, but a slow ant has high precision).
Below are some key advantageous characteristics of tetracoordinates:
Centered
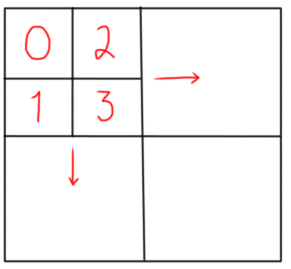
The origin, marked as cell zero above, is centered. This is crucial for later being able to increase scale (outward) and precision (inward), because the current outermost cell is the center/origin of the next level.
Just as in cartesian coordinates with base-10 numbers, where the more significant (leading) and less significant (trailing) digits can be implied zeros (15 = 015 = 0015 = 15.0 = 15.00), tetracoords can behave the same way.
In a system like geohash, however, since there is an even number of cells in a square grid, then the cell designated as zero, the origin, is not centered, but rather at a corner. If you try to scale outward, then that cell will need to be in the same corner of a larger square, thus only allowing scaling in only two directions.
Note geohash doesn’t typically use only 4 cells per level, but I’ve modified slightly for comparison.
Recursive
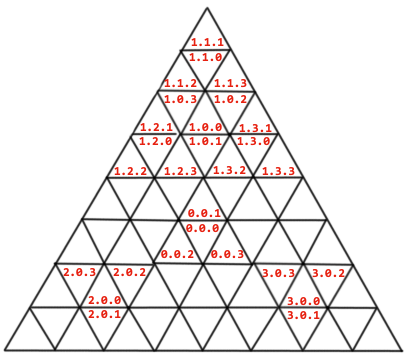
In order to scale inward and outward uniformly, the layout of the cells is recursive, as in geohash.
Base-2/binary compatible
Using four (a power of 2) cells per level makes a tetracoord binary-compatible for efficient storage as a datatype in software.
For example, the base-4 tetracoord 0.1.3 is equal to the binary tetracoord 00.01.11.
Determinate
Just as in geohash, tetracoord cells never overlap, so there is only one coordinate mapping for any cell. However, any theoretical point exactly on the border or vertex between cells is irrational and indeterminate, much in the same way that 3/3 equals 0.9999... equals 1.0.
Mathematical nonnegative scalars
Tetracoord values, though they represent locations in 2-dimensional space, are nonnegative scalar values. This means they don’t need to be represented with multiple components as do cartesian coordinate vectors.
Additionally, and more importantly, tetracoords can still support arithmetic operations (addition, subtraction, multiplication, division, etc), though these operations behave according to laws wholly different from both scalar and vector arithmetic in the number systems we normally use.
However, if the algebraic laws and arithmetic patterns for tetracoords are properly defined, then methods can be written to perform tetracoord arithmetic without the need to convert to a different number space (like cartesian space).
Definition
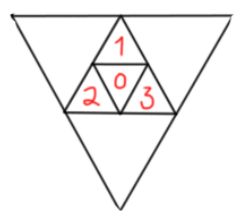
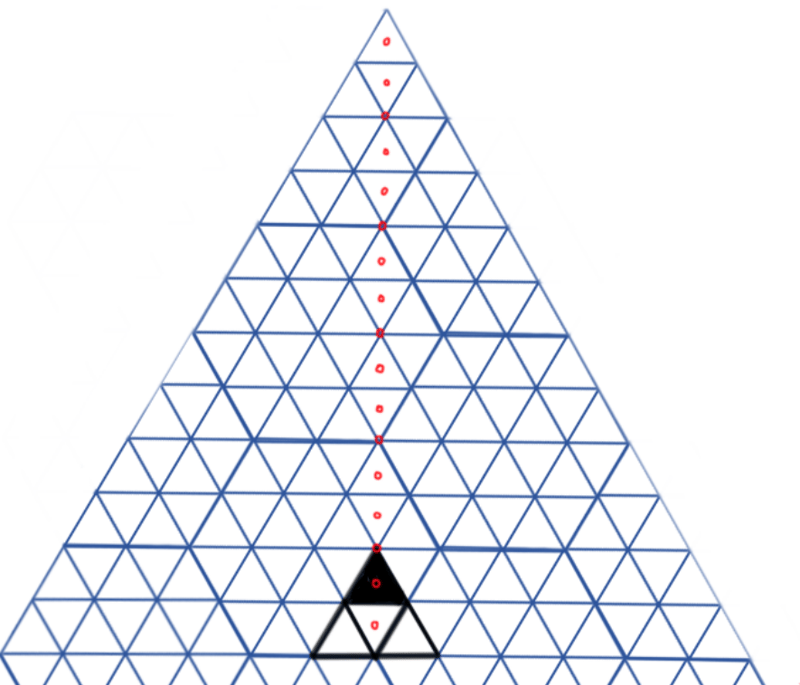
Consider a 2-dimensional space, organized into nested equilateral triangles, like so:
This is the famous Sierpinski Triangle fractal, which ideally would be infinitely large, with an infinite number of subdivisions. In other words, each triangular cell in this infinitely large space is also infinitely small. In practice, however, the implementation of tetracoordinates in a 2D space would always be truncating scale and precision depending on what’s needed.
Now, for creating a tetracoord space, don’t leave the central cells empty, creating a denser (and more boring) version of the fractal. The coordinate value of each cell at each level uses the center cell as 0, and the rest in counterclockwise order, starting with the vertically offset cell, as 1, 2, and 3:
Some cells are left intentionally blank to save myself the effort.
Syntax
Binary and quaternary bases
In this article I switch between base-4 and base-2 representations, which are effectively equivalent.
base-4 (quaternary): 1.3.2.0
base-2 (binary): 01.11.10.00
Of course, other bases could be used for compression or legibility, removing the dot delimiters between levels:
base-4 (quaternary): 1320
base-8 (octal): 170
base-16 (hexadecimal): 78
Delimiters
I use the dot as a place value separator (like ip address byte delimiters), and a double dot after the origin place value (analagous to the point in real decimal numbers).
01.00.10 = 01.00.10.. = 01.00.10..00
..11 = 00..11 = 0..3 (quaternary)
Note that the dot and double dot notation isn’t really necessary when writing tetracoords in base-4, but I’ll use them for consistency.
Algebra
I use a specific notation for algebra, given that at each level there are only four possible values: 00, 01, 10, 11. I use the following variables:
x, y, z, 0
not as placeholders for full tetracoord values, but instead as placeholders for levels within a value. 0 is always 00, but x, y, and z refer to any value other than zero: 01, 10, or 11.
Irrationals
Any point (aka. a cell of infinite precision) on an edge between cells or on a vertex (where edges meet) is an irrational tetracoordinate.
Note that a point along an edge will also be a vertex at a higher specificity.
To denote an irrational number with infinitely repeating digits at each level, I use bar notation, as in:
x̄ ȳ z̄
x.y..y.y.y... = x.y..ȳ
Arithmetic
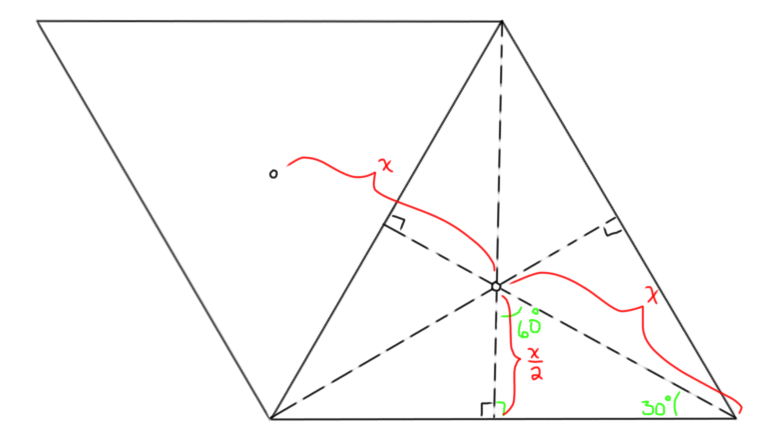
Tetracoords arithmetic is not intuitive compared to traditional, normal, real numbers, and the rules defined below are derived geometrically, given some basic properties of an equilateral triangle:
Please correct me if I’m wrong in the generalizations below! These are key foundational laws for being able to perform tetracoord arithmetic and later use a tetracoord datatype implementation in programs.
Algebraic laws (so far)
These laws are a work in progress and so far only touch on the most basic arithmetic operations.
0 + 0 = 0
0 + x = x
0 - x = 0..x̄
(note that negatives do, in fact, exist,
in order to allow subtraction, but have
equivalent positive values)
-z = 0..z̄
= x..ȳ
= y..x̄
= z.x..ȳ
= z.y..x̄
= z.0..z̄
x + x = x..x̄
= 2x
= y.z..z̄
= z.y..ȳ
= x.0.x..x̄
= x.y.z..z̄
= x.z.y..ȳ
x.y = x.0 - y
x + y + z = 0
x + y = -z
x - y = y.z
Multiples formula
Just as when performing real arithmetic, there are shortcuts that mathematicians have discovered by studying patterns. For example, to compute 5 * 30 you don’t need to compute 5 + 5 + 5 + ... + 5, but can rather do something like (5 * 3) * 10. Along these lines I’ve determined the following formulas to calculate any positive multiple of x:
kis a real number constant.
xandtare tetracoord values, where a subscriptnrefers to a digit within the tetracoord.
po(n)means pattern offset formula.
pl(n)means pattern length formula.Shout out to the math.stackexchange.com community for assisting in the definition of these formulas!
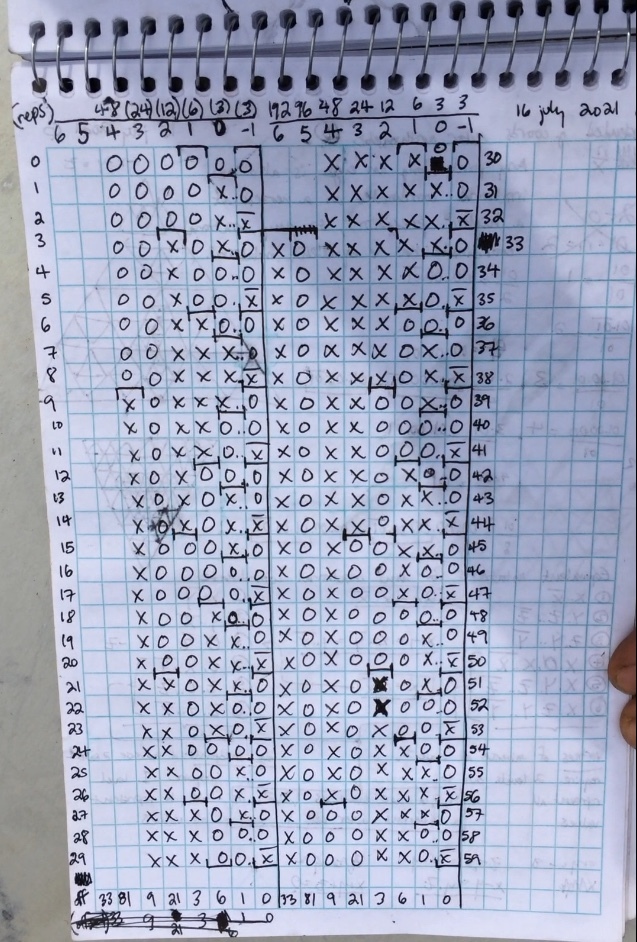
See brainstorming for some messy notes on the derivation.
Below are the results (hopefully) each multiple k*x in set of k = 0, 1, ..., 11:
| k | t |
|---|---|
| 0 | 0.0.0.0.0..0 |
| 1 | 0.0.0.0.x..0 |
| 2 | 0.0.0.0.x..x̄ |
| 3 | 0.0.x.0.x..0 |
| 4 | 0.0.x.0.0..0 |
| 5 | 0.0.x.0.0..x̄ |
| 6 | 0.0.x.x.0..0 |
| 7 | 0.0.x.x.x..0 |
| 8 | 0.0.x.x.x..x̄ |
| 9 | x.0.x.x.x..0 |
| 10 | x.0.x.x.0..0 |
| 11 | x.0.x.x.0..x̄ |
Future research
Explore more advanced tetracoord algebra (multiplication and division, exponents and roots, rules for decomposition and composition at different levels, etc).
Implement a functioning tetracoord datatype in any programming language that leverages its advantages (variable scale and precision, native tetracoord arithmetic, conversion to and from cartesian vector coords).
Create a GUI 2D map navigator that shows tetracoord cells at different specificities and scales and shows equivalent cartesian and tetra coordinates.
Extend a similar system to 3D and possibly further dimensions.


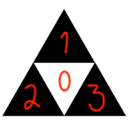


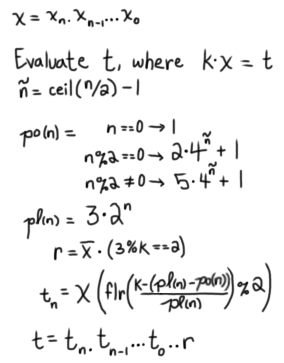


Top comments (1)
reddit/r/tetracoords