In computer science or mathematics, algorithms provide a clear and concise step-by-step process for solving a specific problem. They're commonly used for a variety of tasks, including number sorting, machine learning, or displaying data on a screen. To put things in perspective, think about all the steps you'd take to make a peanut butter sandwich, you'll notice that you follow the same process subconsciously whenever you want to make a peanut butter sandwich, if we were to automate that process, we'd use the same steps. This is the general idea behind algorithms.
In this article, we’ll cover a very popular sorting algorithm the quicksort algorithm, also known as the "Partition Exchange" sort, which provides an effective and efficient method of sorting a list of data. Here's what we’ll cover:
- What is the quicksort algorithm?
- Partition methods
- Hoare's partition method
- JavaScript implementation of quicksort
- Quicksort complexity analysis
- The JavaScript sort method
What is the quicksort algorithm?
The Quicksort algorithm is a divide-and-conquer algorithm created by Tony Hoare and published in 1961. It works by choosing a pivot element (an element in the list that is used to compare other elements in order to divide the list), which can be the first, last, random, or median element, and arranging all of the smaller elements to the left of the pivot and all of the larger elements to the right of the pivot.
It is divide-and-conquer in the sense that each iteration partitions (divides) the input list into two lists, one containing all the elements smaller in value to the left of the pivot, and another containing all the larger elements to the right of the pivot. It then recursively sorts both lists or arrays before recombining them, thereby effectively sorting the list. It is still one of the most efficient general-purpose sorting algorithms available.
There are two things to note here: partition and recursion. Partition is the peanut butter in this sorting algorithm sandwich; it is how we arrange our input list in order, and recursion simply means repeating the algorithm until a condition is met and the list is sorted.
Here are the steps for a quicksort algorithm:
Step 1 - Pick a pivot element depending on the partitioning algorithm you are using
Step 2 - Partition the array based on the pivot
Step 3 - Sort the left partition recursively using quicksort
Step 4 - Sort the right partition recursively using quicksort
Partition Methods
The Quicksort algorithm has several implementations. The partition method used determines these implementations, and they differ in terms of how the pivot element is chosen. The partition algorithm is an essential part of the quicksort algorithm, hence to learn quicksort it is important to understand the partitioning algorithms. There are three kinds of partitioning algorithms available, let's take a look at them:
Naive partition: We create a temporary array in naive partition and store the elements that are less than the pivot first, then the elements that are greater than the pivot. After we create the temp array, we copy it to our original array.
Lomuto partition: The pivot in Lomuto's partition method is the last element. Two pointers are kept for comparison: pointer I is kept, and pointer j is used to scan the array from beginning to end. The scan ensures that any element from the beginning of the array to the (i-1)th index has a lower value than the pivot element, and that any element at any index between I and j has a value equal to or greater than the pivot element. This method allows for more comparison.
Hoare’s partition: The first element is chosen as the pivot in Hoare's partitioning method. It works by initializing two indexes at opposite ends and moving them toward each other until an inversion is found. An inversion is found when a smaller value is on the left side and a greater value is on the right side. When compared to the Lomuto partition, less comparison is done in this method.
For the sake of this article, we would be focused on using Hoare’s partition method. Let's see an example with a visual aid so that we get a feel for how it works.
Hoare's partition method
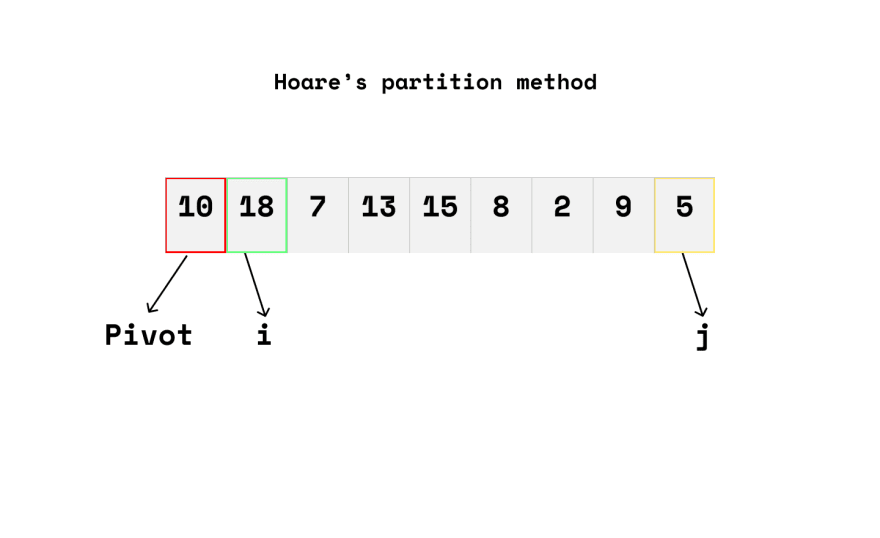
Notice the pivot element and the two indexes i and j that are initialized at both ends of the array in the image above. The index I would look for elements that are greater than the pivot, and the index j would look for elements that are less than the pivot, swapping them as they go.
Here's how it works: index i move a position forward, then checks to see if the element at that index is greater than the pivot. Simultaneously, j would move a position and check if that element is less than the pivot; if both checks are true, they would swap positions.
Let's see a clear example below:
Here's the array we would be working with; [10, 18, 7, 13, 15, 8, 2, 9, 5]
Step 1 is to set our pivot element, which is always the first element in a hoare partition algorithm, and to initialize our i and j indexes, which are the first and last elements, respectively.
Notice how index i moves one step forwards, now we check to see if the element in that index is greater than our pivot, it is, so we have an element to swap.
Now j also checks to see if its element is less than our pivot, since j and i satisfy the condition, they can now swap positions. Now both indexes would move one step forward and continue the process

After the first swap, index i moves one step forward, but this time the element does not satisfy the condition. Notice also that j moves one step forward and its condition is satisfied, but no swap is done until the i’s condition is satisfied. Let’s see that in the next step
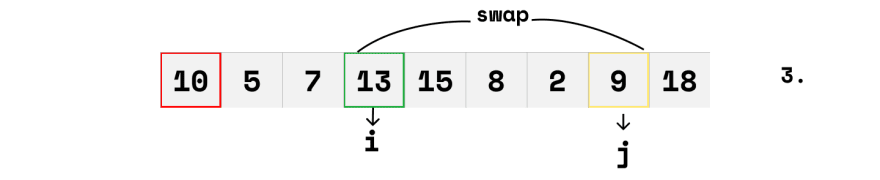
Here i's condition is satisfied so a swap is made.

Here we see the next swap occur after both indexes move forward.
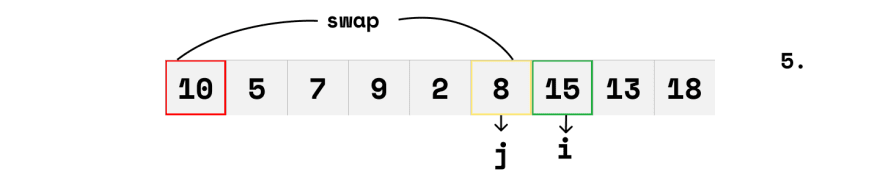
In this step notice that when i moves forward the element (8) does not satisfy the condition so it moves forward again to the element (15) and its condition is then satisfied, j also moves forward and its condition is satisfied. However, we have found the position of the pivot element seeing as i has crossed over and is now greater than j. Now we can swap the element at index j with our pivot element, effectively partitioning the list.
After we have gotten the position of the pivot element, we now have two unsorted list to the left and right of the pivot, to sort these lists we perform quicksort recursively on them.
It’s okay if you don’t understand this now, in the coming section we would see how quicksort uses the partition algorithm and recursion to effectively sort a list.
JavaScript implementation of quicksort
To implement quicksort in JavaScript, we need three functions:
- A swap function that handles swapping the positions of elements like we saw in the previous section. Nothing too fancy just reassigning the indexes of each item.
- A partition function, that handles partitioning of the array, it handles changing the position of elements by calling the swap function.
- A sort function that calls the partition function and performs quicksort recursively until all elements on the left array and right array are sorted.
Note: No new arrays are created in the process of performing quick sort on the given array.
We would be working with the same array we used in the previous section
let unSortedArr = [10,18,7,13,15,8,2,9,5]
Swap function
const swap = (arr, a, b) => {
[arr[a], arr[b]] = [arr[b], arr[a]];
}
Partition function
`
const partition = (arr, first = 0, last = arr.length) => {
let pivot = arr[first]
let pointer = first;
for (let i = first; i < arr.length; i++) {
if (arr[i] < pivot ) {
pointer++;
swap(arr, pointer, i);
}
};
swap(arr, first, pointer);
return pointer;
}`
Quicksort function
`const quickSort = (arr, first = 0, last = arr.length) => {
let pivotIndex = partition(arr, first, last);
if (first >= last) return arr;
quickSort(arr, first, pivotIndex);
quickSort(arr, pivotIndex + 1, last);
return arr;
};
let sortedArr = quickSort(unsortedArr);
console.log(sortedArr);`
Quicksort complexity analysis
Let's talk about the time and space complexity of the Quicksort algorithm now that we know how to implement it.
Note: quicksort performs differently based on how we choose the pivot element and how we divide (N) elements where (N) is the input size.
Best case time complexity
The best case time complexity for a quicksort algorithm is O(nlogn), but it is not possible for us to achieve this, randomly we can, but it is rare.
Average time complexity
Quicksort follows a divide and conquer procedure, now say we partition the input list (N) from the middle always this means that we’re dividing by 2, and to get to 1, it would go something like this;
(N/2/2/2/2/2) for every partition we make, we can turn this to (N/2^k = 1) which turns to (N = 2^k) when we cross multiply. We finally arrive at (k = logn2) where 2 is a base.
Therefore Quicksort takes O(nlogn) time in expectation to sort an array of n distinct elements, averaged over all n! permutations of n elements with equal probability.
Worst case time complexity
The worst case time complexity of quicksort is O(n^2) because for an already sorted list partitioning would always happen at the beginning of the list.
Space complexity
The space complexity for this algorithm is O(N) because we are not creating a new array other than the given array therefore Space complexity will be in the order of N
Here's an excellent article that dives deep into the complexity analysis of the quicksort algorithm.
JavaScript sort() method
JavaScript offers a simple and easy-to-use inbuilt sorting method, that we can use to sort a list. To use it we simply call the method on the array like so:
let arr = [4,7,3,9,2,5,8]
console.log(arr.sort())
We would get our array sorted in ascending order
// [2,3,4,5,7,8,9]
So what is the problem with using this method, why do we still need to use quicksort?
The issue is with the way the array elements are sorted, in Chrome's V8 Engine, the default sort() method used by JavaScript uses insertion sort, while Mozilla Firefox and Safari use merge sort. This method, however, is inefficient when sorting a sizable number of elements. In that case quicksort is the best method for large sets of data.
Conclusion
In this article, we've gone over the theory behind Quicksort to see how it works and the different partition methods that can be used with quicksort we also saw how it can be implemented recursively using JavaScript.




Top comments (0)