Graphs

Today we will be talking about the two ways we can search through the graph data structure. First a rephresher on graphs. Graphs are used to describe a model that shows the route from one node to another node. Graphs consist of multiple nodes connected in between by edges.
Unlike trees, graphs are not hierarchical. There is no parent nodes, just nodes with relationships between other nodes. Graphs can be undirected, which means that the relationship of any 2 nodes connected by an edge is a symmetrical relationship. Graphs can alternatively be directed, which means there is an asymmetrical relationship between nodes that are connected by an edge. In the image below, fig 1 is undirected meaning it has no direction to an edge, while figure two has direction to the edge. Now we will explore the differnce bewtween the search methods.

Depth First Search(DFS)

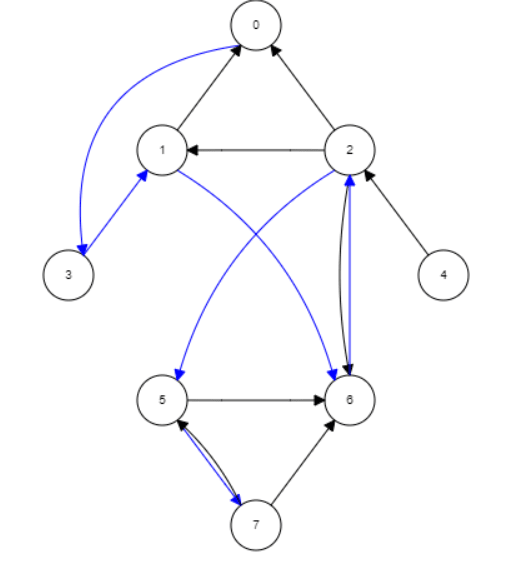
The first method we will talk about is Depth First Search. DFS is a recursive algorithm for searching all the vertices of a graph. DFS uses stacks in its implementation. This search method takes the scenic-route deep through the nodes. the search will start off at the first node and transverse down through the connecting edges all the way to the node that have no child attached or end node, then it will travese its way back up until it finds a new path to get to the end.

In the image above we will start off at node 0 and jump to node three then from node three to node one then to node 6 and so on.

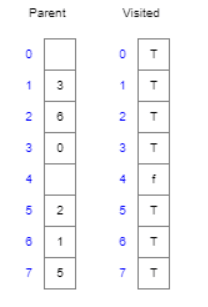
With this method if we were looking for node 4 it would take a while to find because of the algorithm it uses to search. Because this graph has a property of being cyclical, meaning it can be routed back to a node it already visited, we can implement a storage for all of the nodes it visits.

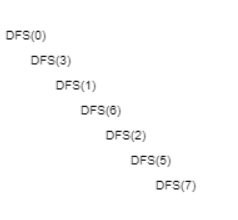
In the image above we have a call stack of the path the graph takes in its execution. Once it reaches the end of a node it will use this call stack to traverse its way back up to find a new path to the end.

With the stack array above we will have the value set to a boolean so that everytime we vist a node we will set the node value equal to true. this helps to stop our graph from going back to the same node twice in its search and slowing down our code. A non-recurssive code implementation could look like this.

Breadth First Search(BFS)

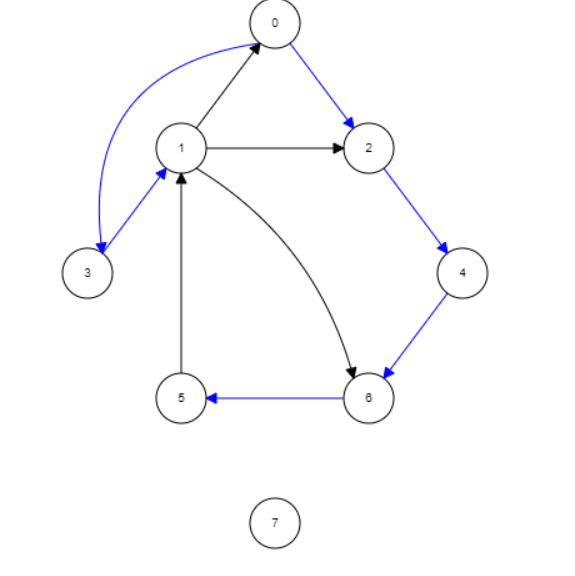
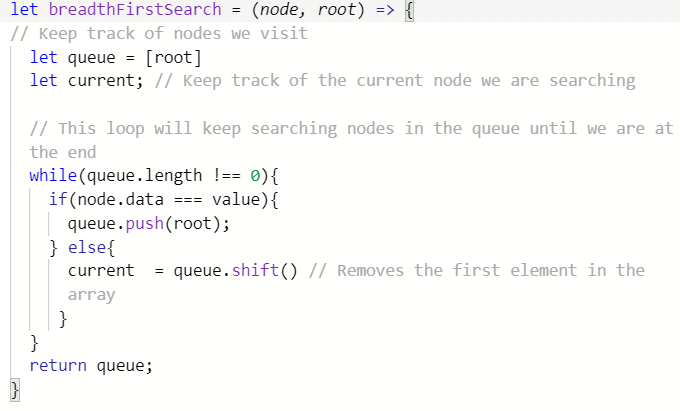
Breadth First Search works its way across the nodes before going down. The BFS algorithm likes to stay as close as possible to the starting point, and stores it's values in a queue instead of a stack. As it search a node if its not the value we want it shifts that node out of the queue array.This algorithm is usually faster than a BFS because the it checks each node edge before moving down the graph. so there is no need to come back an search throught the graph.

Image of breadth first search

In the image above if we are looking for node 4 we will find it quicker using this method because we will check the neighboring nodes before moving pass them and at that point we will find it. heres a basic code implementation

Conclusion
In conclusion, Depth First Search is a more through search method that takes more time to get a result. the best use for this algoritm isif you want to check deep in your data and not iss anything. If you just want to find your reult faster the Breadth First Search algorithm will be good unless what you're looking for is towards the end without a good path to it from the first node.