The Byes's Table solution that many Lecturers find difficult to explain.
Bayes'rule has been one of the oldest and the most technical method use in solving probability. let's one example of the Byes critical question that almost turn many lecturer to demon in class.
Example
Solution
Explanation
Now You can study the solution from morning till night and still not understand what is happening.
here is the explanation.
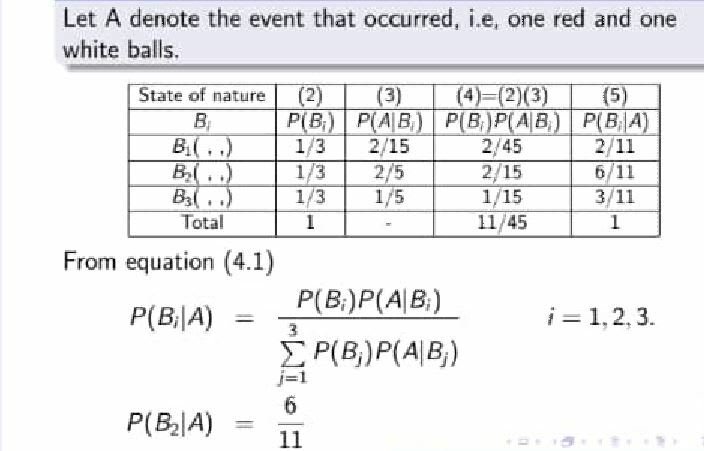
Column1: this contain the number of Basket or places where the event could occured. in this question we have just 3. as you can see from the question so we labeled it B1,B2,B3 and Total.
Column2: here is where we write the probability for each basket. since we have just 3baskets it is very easy to know that the probability of selecting each basket is 1/3.
the total is the sum of all.
column3: Here we find the probability of selecting red and white from the Baskets(B1,B2,B3). the solution is below.
Solution
firstly note that the event is without replacement.
let R means Red and W means White
Pr(R and W without Replacement) = pr(R then W) OR pr(W then R).
NOTE: we have to consider two since we don't know which one is first selected.
Now,
let A denote the event that occurred i.e one red and one white(pr(A|B1))
Prob(A|B1)= pr(B1|RnW) OR pr(B1|WnR)
pr(B1|RnW)=2/6*1/5=1/15(note without replacement we minus 1 for every next event.)
pr(B1|WnR)=1/6*2/5=1/15 (this time White is selected first.)
Prob(A|B1)=1/15 +1/15=2/15.
Now for B2
we already know the formula. so we just do a little adjusment.
Prob(A|B2)= pr(B2|RnW) OR pr(B2|WnR)
pr(B2|RnW)=3/6*2/5=1/5(note without replacement we minus 1 for every next event.)
pr(B1|WnR)=2/6*3/5=1/5 (this time White is selected first.)
Prob(A|B1)=1/15 +1/15=2/5.
Now for B3
we already know the formula. so we just do a little adjusment.
Prob(A|B3)= pr(B3|RnW) OR pr(B3|WnR)
pr(B3|RnW)=1/6*3/5=1/10(note without replacement we minus 1 for every next event.)
pr(B1|WnR)=3/6*1/5=1/10 (this time White is selected first.)
Prob(A|B1)=1/10 +1/10=2/10 =1/5.
the total of all is not important you can leave that or add it too.
Yeah that is the most difficult part. Now let's proceed to the next column
column4
looking at the heading of the table you will discovered that we are trying to simplify Bayes' Rule.
so we multiply column2 and column3 together like the following.
A. 1/3*2/15 = 2/45
B. 1/3* 2/5 = 2/15
C. 1/3*1/5=1/15
the last is the sum of the three value.
Can you see?? that is as easy as one plus one.
now let's do the last column.
Column5
this column is the solution that satisfied the Bayes'formula.
P(Bi|A)=P(Bi)P(A|Bi)/{P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3)+P(B4)P(A|B4)......+P(Bn)P(A|Bn)}
so, P(B1)P(A|B1)=(2/45)/{2/45+2/15+1/15}.
P(B1)P(A|B1)=(2/45)/{11/45}
P(B1)P(A|B1)=2/11
for the second one
P(B2)P(A|B2)=(2/15)/{2/45+2/15+1/15}.
P(B2)P(A|B2)=(2/15)/{11/45}
P(B2)P(A|B2)=6/11
For the third one
P(B3)P(A|B3)=(1/15)/{2/45+2/15+1/15}.
P(B3)P(A|B3)=(1/15)/{11/45}
P(B3)P(A|B3)=3/11
the last is the total of all.
Now the most beautiful thing about this table is that it solve so many problem at once.
the question ask for the probability of chosen Red and White from B2. and that is what we get in the last column. i.e 6/11.
Had the question is from the first Basket then our answer would have be 2/11. while 3/11 will be the answer for the third basket.
I hope you find this article helpful and intresting ??
you can chat me up on whatsapp(07045225718) if you have any question you want to ask. it's your guy Maxwizard.
You can also read



Top comments (0)