In an era when processors were sluggish and memory scarce, programmers had to come up with ingenious little tricks to accelerate their software, the king of which was bit manipulation. Yet as technology has progressed, our faster processors and sophisticated programming languages have relegated these hacks to obscurity. Though they no longer offer the same tangible performance advantages, rediscovering them can enrich our perception of how logic and creativity exist in the world of coding.

We're set to take a deep dive into some of my favorite bit hacks, exploring and understanding their underlying mechanics. As we delve into the intricacies of each trick my hope is that you'll gain a richer understanding of what's happening beneath the surface of your code. At minimum I hope to install in you an admiration for the cleverness encapsulated in these hacks.
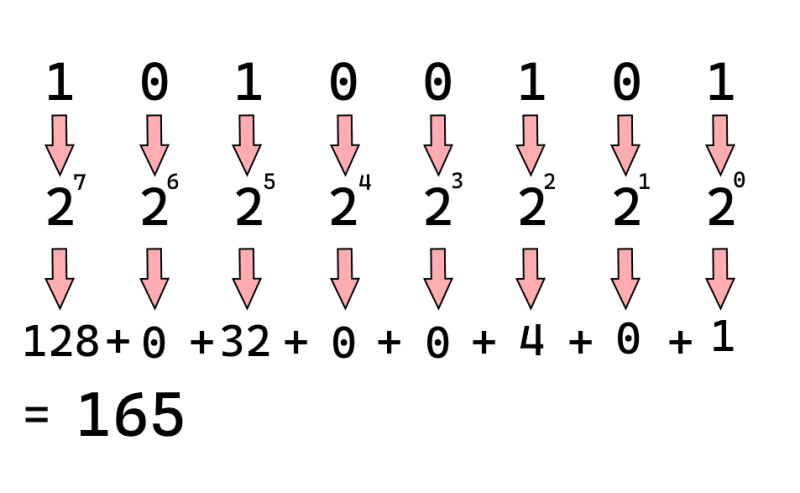
First lets take a quick review on how binary numbers work:

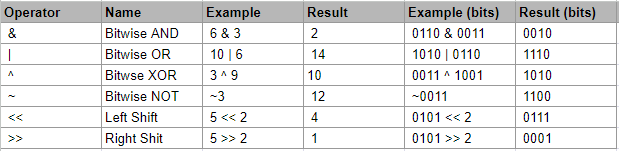
We'll talk about the specific bitwise operations we use for each problem, but feel free to reference this table or check the Wikipedia page page for more details:

Example Problems

Even Or Odd?

Every coder's journey starts somewhere, and often one of the first stops is the basic math problem: "Is this number even or odd?" It's a rite of passage, teaching some foundational concepts, providing some quick feedback, and being just fun enough to be engaging.
First the classic approach:

bool isOdd(int number)
{
    if(number % 2 == 0)
    {
        return false;
    }
    else
    {
        return true;
    }
}

In this version, we're checking if the number is divisible by two (the textbook definition of evenness) - no remainder, no oddness. But let's check out how a bit based solution works:

bool isOdd(int number)
{
    return number & 1;
}

Now that's an elegant solution! No comparison, division/modulo, or jump required. A simple AND that outperforms the conventional method with ease.

What our code is doing bitwise is checking if the final bit in the number is on. In the same way that we can know a number is odd in base 10 by considering the final digit (checking if it is 1,3,5,7, or 9), we can do so in binary - but here we only have two digits to consider. If the digit is 1 then we know it to be odd, otherwise it is even. This AND statement gives us the final bit, which yields us a 1 in the case the number is odd, and a 0 otherwise. Conveniently, most languages will implicitly convert those to true and false respectively. As an exercise, you can verify this solution works even using negative numbers in two's complement!

Determining The Sign of a Number

The challenge of identifying a number's sign is as ancient as it is pervasive. We often need to handle positive and negative numbers differently, requiring us to discern the sign of a given number. Let's first look at a simple modern approach.

int sign(int x)
{
    if(x < 0)
    {
        return -1;
    }
    else if(x == 0)
    {
        return 0;
    }
    return 1;
}

This is a standard solution that's quite simple to arrive at. It's also quite long and has some if statements. Next let's look at the fastest bit based version:

int sign(int x)
{
   return x >> 31;
}

Introducing The Right Shift Operator (>>): A shift operator is one the most simplistic operations our computer can do. It simply takes all of the bits in a number and moves them to the left. An arithmetic shift (the kind we use) also copies the neighbor bit when we add new digits. Let's look at an example:

00101010 >> 1  = 00010101 - move all of our bits to the right one space
10110101 >> 3  = 11110110 - move all of our bits to the left three spaces - note because a 1 was in the leftmost spot our 3 new digits to the left are also 1.

Remarkably simple isn't it? This solution relies on certain conditions to work: it requires the int to be 32 bits, and for the most significant bit (left-most bit) to represent the sign of the number. Given that most modern languages utilize the arithmetic shift, when a new bit is added to one side it replicates the adjacent bit. Thus, if x is negative, the resultant number will in binary be thirty-two 1s in binary, translating to -1 due to two's complement representation. If x is non-negative, then the leftmost bit is 0 and all new bits given by the shift operation also become 0, leaving us with 0. So, if x is negative this code returns -1; otherwise it returns 0. As compact and efficient as this solution may be, it's important to note its underlying assumptions and that it doesn't return 1 when the number is positive, unlike our initial solution.

Can we find a compromise? A method that's quick and succinct, and aligns with the output of our original code? With a few tweaks to our existing code we can:

int sign(int x)
{
    return x!= 0 | (x >> 31);
}

Introducing The Or Operator (|) - The OR operator combines the bits of two numbers, producing a new number with a 1 in any position where either of the original numbers had a 1. Let's look at an example:

11001100 OR (|) 204
01010101         85
---------------------------
11011101        221

Let's go over all three scenarios here:

1. x is positive: Then the left side of our OR becomes 1, and the right side becomes 0, resulting in 1.
2. x is zero: Then the left side becomes 0, and the right side becomes 0, resulting 0.
3. x is negative: The left side becomes 1, and the right side becomes -1, yielding -1.

However, like our previous solution, bear in mind this method hinges on the same set of assumptions about the language and hardware. While this approach might save us a few assembly instructions, it compromises platform-agnosticism. Therefore in the modern day or portable code, this solution is not advisable.

We can achieve a platform-agnostic result by utilizing comparison operators, yielding the same results as the original method

int sign(int x)
{
   return (x > 0) - (x < 0);
}

This solution does operate agnostically. I'll leave verification of this solution as an exercise to the reader - here's a hint: In most programming languages the boolean value true is converted to 1 and false is converted to 0.

Swap Two Numbers

Programmers love a good reshuffle! We may not always realize it, but every time we sort an array or a list we're engaged in a continuous process of swapping two variables. Let's recall the traditional way of swapping two numbers:

//setup
int a = 3;
int b = 5;

int tmp = a;
a = b
b = tmp;

Or in the context an a list:

int array[] = {a,b};
int tmp = array[0];
array[0] = array[1];
array[1] = tmp;

The typical swap sees us create a temporary variable to help a and b switch places. But what if we could avoid using a temporary variable? With integers we can use a nifty bit trick to swap them:

int a = 3;
int b = 5;
a = a ^ b;
b = a ^ b;
a = a ^ b;

Introducing The XOR Operator (^) - The XOR operator combines the bits of two numbers, producing a new number with a 1 in any position where exactly one of the original numbers had a 1. Let's look at an example:

11001100 XOR (^)  204
01010101          85
---------------------------
10011001          153 

Now that looks quite cool! What's happening here is we are using the XOR operation to swap a and b. Lets break it down into a few different variables to see what's happening.

int a = 3;
int b = 5;
int r1 = a ^ b;
int r2 = r1 ^ b = (a ^ b) ^ b;
int r3 = r1 ^ r2 = (a ^ b) ^ (a ^ b) ^ b;

How does this simplify? Well the XOR operation has three useful properties we make use of: it's commutative (A ^ B = B ^ A), self-annihilating (A ^ A = 0), and has a zero identity (0 ^ A = A). Using these properties we can simplify the above:

int a = 3;
int b = 5;
int r1 = a ^ b;
int r2 = r1 ^ b = (a ^ b) ^ b = a ^ 0 = a;
int r3 = r1 ^ r2 = (a ^ b) ^ (a ^ b) ^ b = (a ^ a) ^ (b ^ b) ^ b = 0 ^ 0 ^ b = 0 ^ b = b;

And just like that we've swapped a and b all without a temporary variable. While this trick might not be useful in your everyday coding, it's a neat way to trade out an extra memory allocation for spending more CPU cycles.

Conclusion

So why don't we use these?

While these bit hacks are clever and may simplify the bytecode instructions, we rarely observe significant performance boosts implementing them today. This is primarily due to advancements in code compilers, and contemporary CPU features. Modern compilers are adept at uncovering and implementing these sorts of optimizations in your code, often without your explicit knowledge.

Furthermore, the complexity of today's CPU capabilities - such as branch prediction, SIMD, out of order execution, and instruction level parallelism to name a few - renders the performance of a program far more intricate than simply associating a particular cycle count with each instruction type.

Adding to their limited applicability is the fact that even if we wrote a function that managed to save 5 cycles each time its run, on a modern processor running at 3GHz, we'd need that function to execute several hundred thousand times to witness just a milliseconds worth of time savings. These aptly named micro-optimizations are rarely worth pursuing over macro level optimizations.

So when should we use these?

These cunning bit manipulation tricks lend themselves well to a style of programming I call cheeky coding. Rather than focusing on writing quality code, cheeky coding emphasizes showcasing your skill in a dazzling, if somewhat mischievous, manner. The allure of bit tricks is their ability to obfuscate your code, irk your coworkers, and reduce its readability, all while maintaining a thin veneer of utility. The only time that I might recommend using this style would be in an interview setting, where it could impress your interviewer, or annoy them - ideally both.