Bubble sort is the simplest sorting algorithm, compares the adjacent value and swap the element based on the condition.

In ascending order sorting basicly what it do is, comapres the two values and change the position, iterate it through the values and place the highest value at the end.
For this example we are taking this value as input
Values list -- > [6, 5, 3, 1, 8, 7]
Tracing
STAGE 1
Input
[6, 5, 3, 1, 8, 7]
compare position 0 and 1 values
---> 6>5 position 0 is greate than 1, swap it
[5, 6, 3, 1, 8, 7]
compare position 1 and 2 values
---> 6>3 position 1 is greate than 2, swap it
[5, 3, 6, 1, 8, 7]
compare position 2 and 3 values
---> 6>1 position 2 is greate than 3, swap it
[5, 3, 1, 6, 8, 7]
compare position 3 and 4 values
---> 6>8 position 3 is less than 4, no swap
[5, 3, 1, 6, 8, 7]
compare position 4 and 5 values
---> 8>7 position 4 is greate than 5, swap it
[5, 3, 1, 6, 7, 8]
LAST POSITION VALUE 8 IS LOCKED
STAGE 2
Input
[5, 3, 1, 6, 7]
compare position 0 and 1 values
---> 5>3 position 0 is greate than 1, swap it
[3, 5, 1, 6, 7]
compare position 1 and 2 values
---> 5>1 position 1 is greate than 2, swap it
[3, 1, 5, 6, 7]
compare position 2 and 3 values
---> 5>6 position 2 is less than 3, no swap
[3, 1, 5, 6, 7]
compare position 3 and 4 values
---> 6>7 position 3 is less than 4, no swap
[3, 1, 5, 6, 7]
LAST POSITION VALUE 7 IS LOCKED
STAGE 3
Input
[3, 1, 5, 6]
compare position 0 and 1 values
---> 3>5 position 0 is less than 1, no swap
[3, 5, 1, 6]
compare position 1 and 2 values
---> 5>1 position 1 is greate than 2, swap it
[3, 1, 5, 6]
compare position 2 and 3 values
---> 5>6 position 2 is less than 3, no swap
[3, 1, 5, 6]
LAST POSITION VALUE 6 IS LOCKED
STAGE 4
Input
[3, 1, 5]
compare position 0 and 1 values
---> 3>1 position 0 is greate than 1, swap it
[1, 3, 5]
compare position 1 and 2 values
---> 3>1 position 1 is less than 2, no swap
[1, 3, 5]
LAST POSITION VALUE 5 IS LOCKED
STAGE 5
Input
[1, 3]
compare position 0 and 1 values
---> 3>1 position 0 is less than 1, no swap
[1, 3]
LAST POSITION VALUE 3 IS LOCKED
Sorted result 1, 3, 5, 6, 7, 8
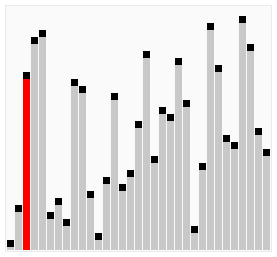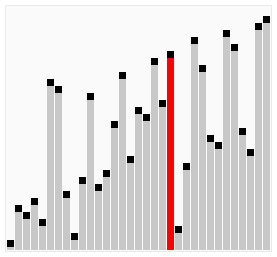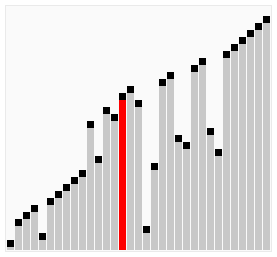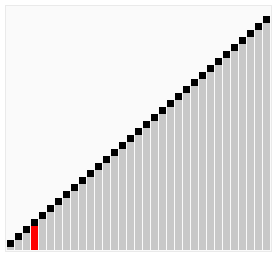
In this example we are using the python for loop to iterate over the list values, create a python function called bubbleSort where the logic for bubble sort will be written.
def bubbleSort(k):
last = 0
for i in range(0,len(k)):
# reduce the last value to avoid over lapping
for j in range(0,len(k)-1-last):
# compare the adjustent value
if k[j] > k[j+1]:
k[j], k[j+1] = k[j+1], k[j]
last+=1
print(k)
return k
k = [3,40,2,0,10]
bubbleSort(k)
"""
result
[3, 2, 0, 10, 40]
[2, 0, 3, 10, 40]
[0, 2, 3, 10, 40]
[0, 2, 3, 10, 40]
[0, 2, 3, 10, 40]
[0, 2, 3, 10, 40]
"""
Another method
If the values are already sorted or in the mid of the process if it get sorted then you don't have to do the process till the end. We can stop it when values got sorted.
def bubbleSort(k):
last = 0
for i in range(0,len(k)):
# when the list is already sorted, its better to stop this will increase the process time
done = True
# reduce the last value to avoid over lapping
for j in range(0,len(k)-1-last):
# compare the adjustent value
if k[j] > k[j+1]:
k[j], k[j+1] = k[j+1], k[j]
done = False
if done:
break
last+=1
print(k)
return k
k = [3,40,2,0,10]
bubbleSort(k)
"""
result
[3, 2, 0, 10, 40]
[2, 0, 3, 10, 40]
[0, 2, 3, 10, 40]
[0, 2, 3, 10, 40]
"""
You can see the difference in the result first method run till the end, in second method once the list sorted, it stop.
Time Complexities
Bubble sort has a worst-case and average complexity of О(n2), Best case of O(n) if the values already sorted.



Top comments (0)