Graph problems play a pivotal role in various fields, from computer science to logistics. Understanding and solving these problems require a diverse set of algorithms. In this blog post, we'll explore some fundamental graph problems, shedding light on their significance and presenting solutions that cater to different scenarios.
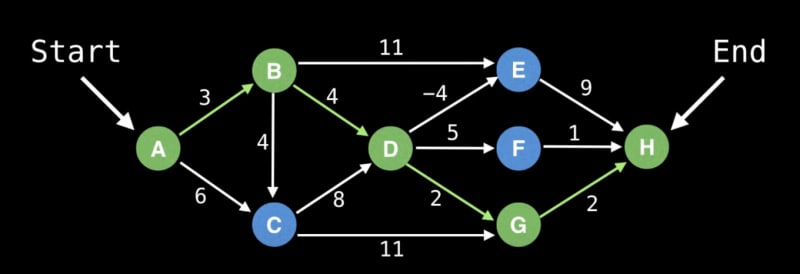
Shortest Path Problem:
The shortest path problem revolves around finding the most efficient route between two nodes in a graph. Various methods can tackle this problem, depending on the nature of the graph:
BFS (Unweighted Graph): Ideal for unweighted graphs, BFS systematically explores neighbors to discover the shortest path.
Dijkstra's Algorithm: Efficient for graphs with non-negative weights, Dijkstra's algorithm optimally finds the shortest path.
Bellman Ford: A versatile algorithm that accommodates graphs with negative weights.
Floyd-Warshall: Suitable for all-pairs shortest path problems, handling both positive and negative weights.
A*: Combines aspects of Dijkstra's and greedy algorithms, optimizing pathfinding with heuristics.
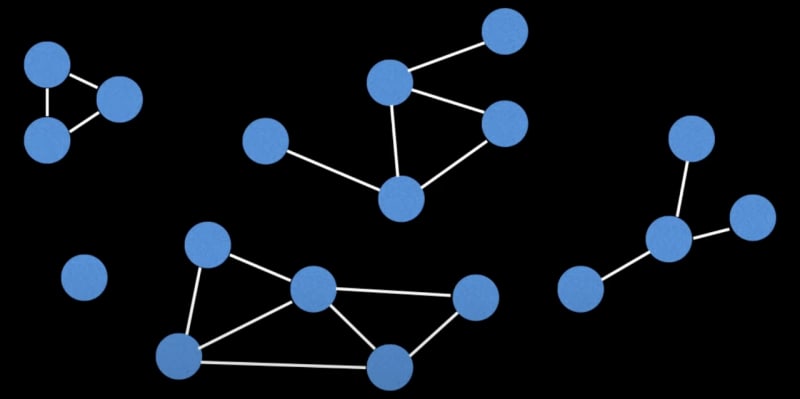
Connectivity:
Determining connectivity involves establishing whether a path exists between two nodes. Here are methods tailored for different scenarios:
Union Find Data Structure: Efficiently detects connectivity in disjoint sets.
DFS (Depth-First Search): Systematically explores the graph's depth to ascertain connectivity.
BFS (Breadth-First Search): Unveils connected nodes layer by layer, aiding in connectivity analysis.
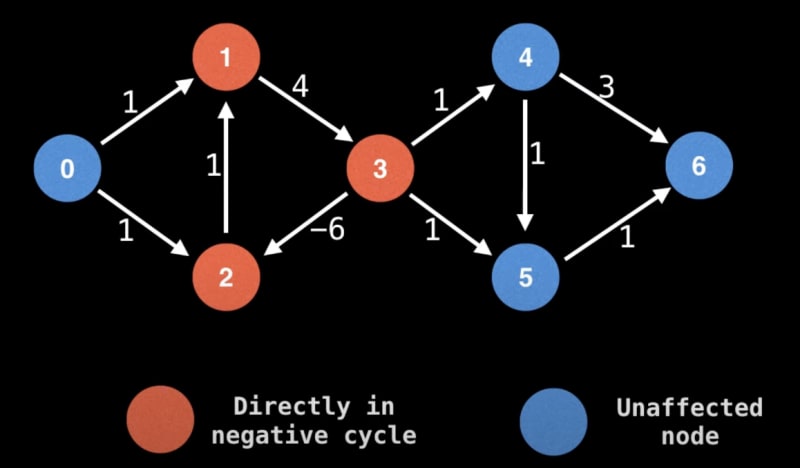
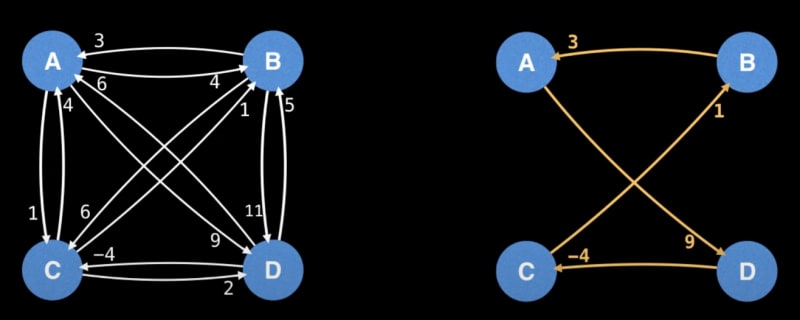
Negative Cycle:
Identifying negative cycles in weighted directed graphs is crucial. The following algorithms are adept at handling this task:
Bellman Ford: Detects negative cycles and their locations in the graph.
Floyd-Warshall: Extensively applicable, it identifies negative cycles in the graph.
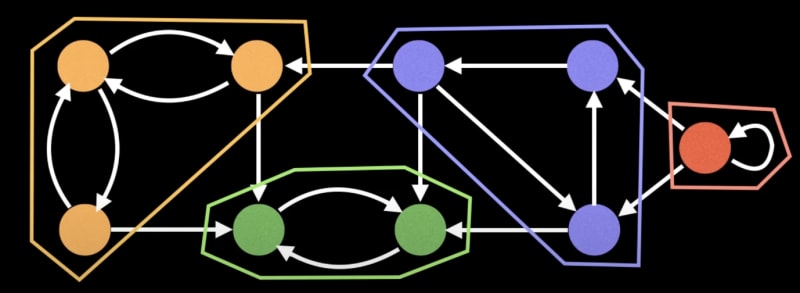
Strongly Connected Components:
Strongly connected components (SCC) are self-contained graph portions in directed graphs. The following algorithms excel in identifying SCC:
Tarjan's Algorithm: Effectively identifies SCC in linear time.
Kosaraju's Algorithm: Divides the graph into SCC, offering a comprehensive understanding.
Travel Salesman Problem:
The Traveling Salesman Problem (TSP) challenges us to find the shortest path visiting all cities exactly once. As an NP-hard problem, TSP requires sophisticated approaches:
Held-Karp with DP (Dynamic Programming): Optimally solves smaller subproblems, building up to the complete solution.
Branch and Bound: Systematically explores potential solutions, pruning branches for efficiency.
Other Approximation Algorithms like Ant Colony Optimization: Leverages heuristic methods for practical solutions.
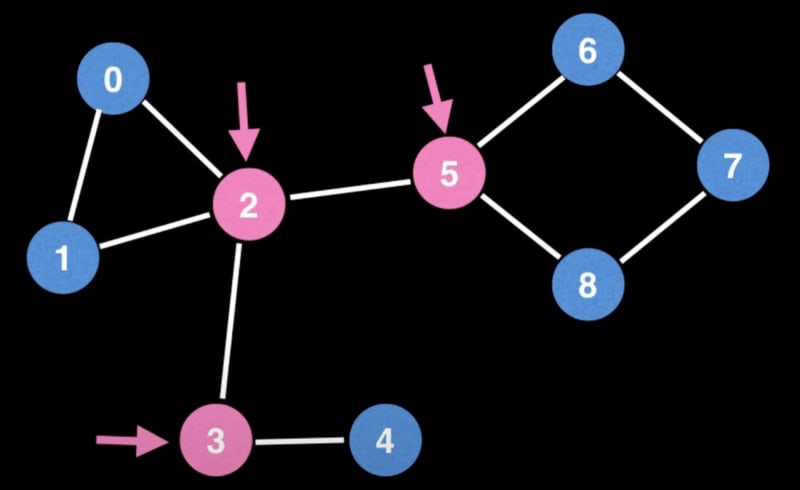
Bridges and Articulation Points:
Bridges and articulation points highlight vulnerabilities in a graph:
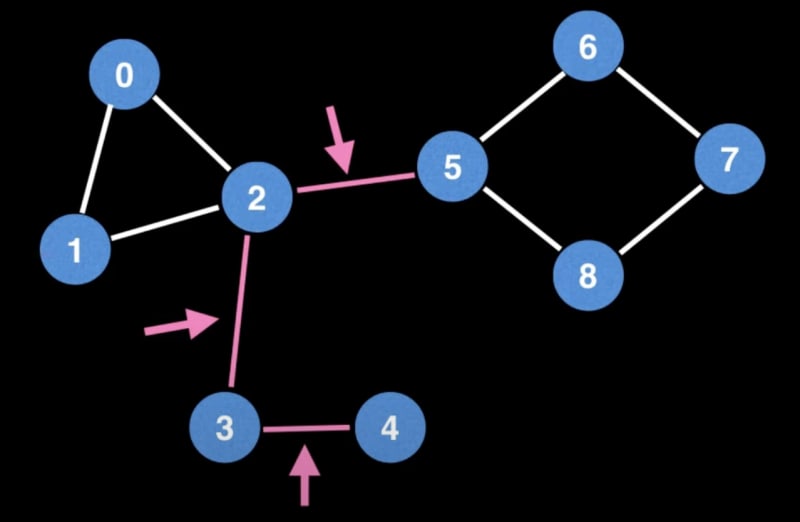
- Bridges: Removing them increases the number of connected components, exposing critical edges.
- Articulation Points: Their removal amplifies the number of connected components, signaling key nodes in the graph's structure.
These indicators often reveal weak points, bottlenecks, or vulnerabilities in a graph.
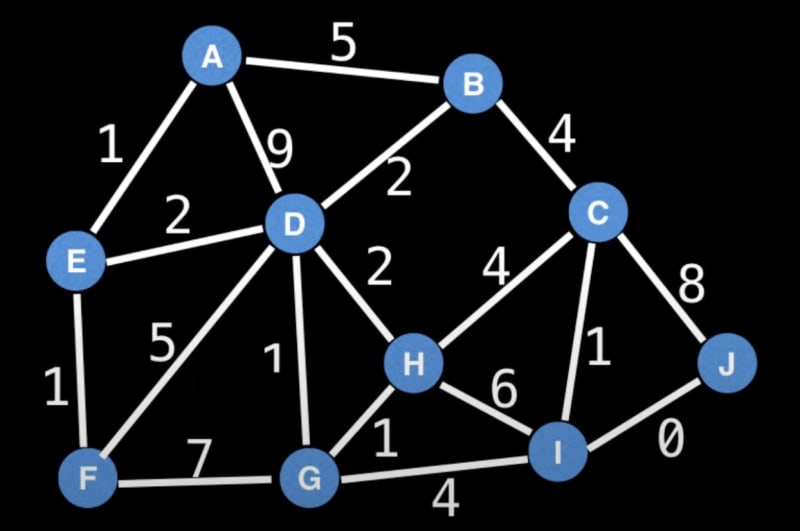
Minimum Spanning Tree:
A Minimum Spanning Tree (MST) connects all vertices with the least total edge weight and no cycles. Algorithms for finding MST include:
Kruskal's Algorithm: Greedily selects edges with the smallest weights to construct the MST.
Prim's Algorithm: Builds the MST incrementally, selecting the lightest edge at each step.
Boruvka's Algorithm: Iteratively adds edges to the MST until all vertices are covered.
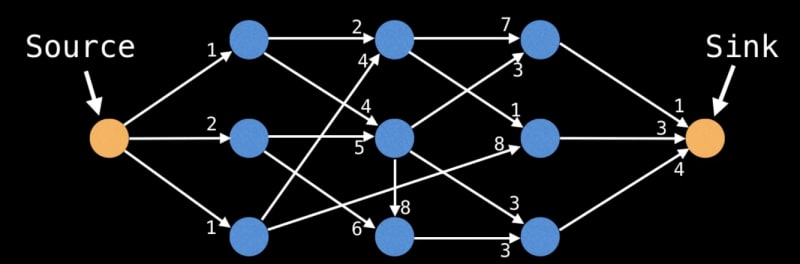
Network Flow (Max Flow):
Determining the maximum flow through a network is crucial in various applications:
Ford Fulkerson Algorithm: Augments flow paths to achieve maximum flow.
Edmonds-Karp Algorithm: A specialized implementation of Ford Fulkerson using BFS for efficient augmentation.
Dinic's Algorithm: Optimizes the augmentation process, enhancing efficiency.
Understanding these graph problems and their solutions equips you with a powerful toolkit for tackling diverse challenges in computer science, optimization, and beyond. Whether you're navigating paths, exploring connectivity, or optimizing flows, these algorithms form the backbone of computational problem-solving.







Top comments (0)