 Given an array of integers nums and an integer k, return the number of contiguous subarrays where the product of all the elements in the subarray is strictly less than k.
Given an array of integers nums and an integer k, return the number of contiguous subarrays where the product of all the elements in the subarray is strictly less than k.
Example 1
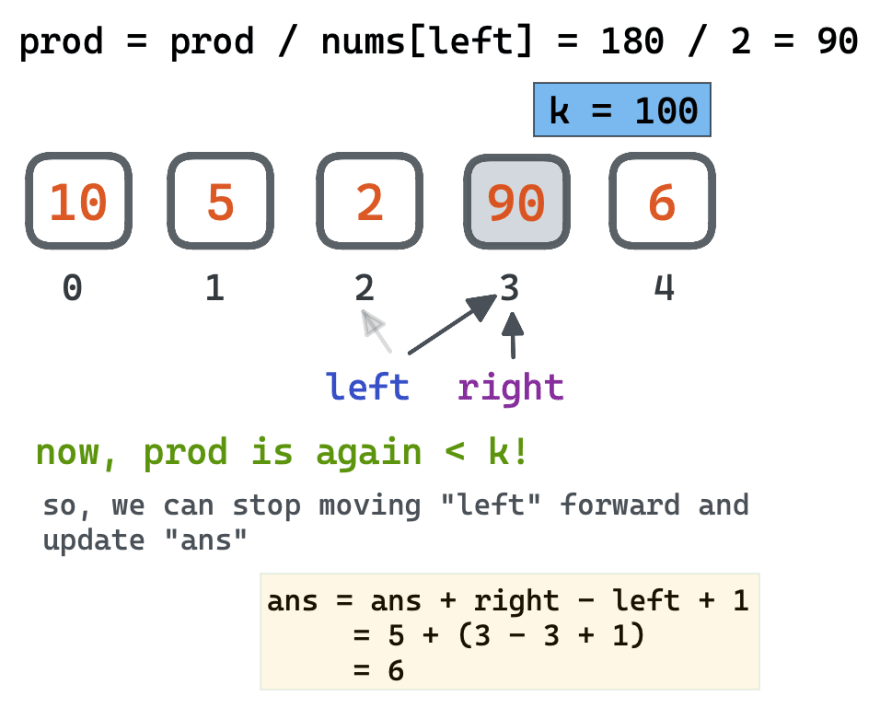
Input: nums = [10,5,2,6], k = 100
Output: 8
Explanation: The 8 subarrays that have product less than 100 are:
[10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6]
Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.
Example 2
Input: nums = [1,2,3], k = 0
Output: 0
Constraints
1 <= nums.length <= 3 * 104
1 <= nums[i] <= 1000
0 <= k <= 106
Editorial
The simplest way to think of this problem is taking cumulative product from an index up to the end of the array. Then check if any of those products < k or not. We will have to do this for each index. Then, for any subarray product < k, we can count the number of subarrays and find the result by adding up those counts.
But this approach will cost us O(N2) [O N square] runtime which is not efficient and we don't want that! So, let's not waste time on it. The better approach to solve this problem is to .... read more
Editorial source: foolishhungry blog


Top comments (0)