Intro

A blog on how you can traverse a graph by using the Depth First Search (DFS) algorithm.

depth first search (DFS)

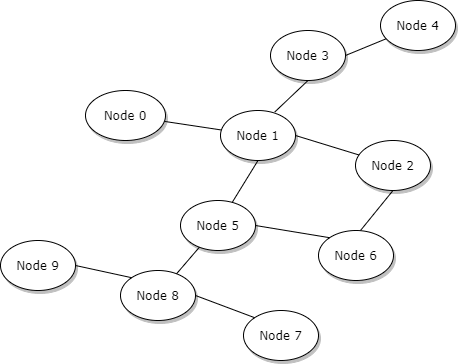
I will try to explain the algorithm through an example (is based on the bellow graph)

the above graph can be represented using an adjacent list (see about graph representation here: more on adjacent list)

var graph = [[1],
             [2, 3, 0, 5],
             [1, 6],
             [1, 4],
             [3],
             [1, 6, 8, 7],
             [5, 2],
             [5, 8],
             [5, 7, 9],
             [8]];

In a graph search you have to first select a node to start the search.
Let's say that we select to start the search form the node with id 1.

• node 1 is marked as a visited node (we mark each node that we visited in order to avoid the cycles)
• node 1 has 4 adjacent nodes, nodes 2, 3, 0 and 5
• DFS selects node 2 as the next node to visit, node 2 marked as visited node [so far visited: 1 ,2]
• now node 2 has two adjacent nodes, node 1 and 6 node 1 has marked as visited so the algorithm continues the search by visiting the node 6
• node 6 marked as visited [so far visited: 1 ,2, 6], node 6 has 2 adjacent nodes: node 2 and 5
• node 2 is marked as visited, so DFS continues the search by visiting the node 5
• node 5 marked as visited [so far visited: 1 ,2, 6, 5], node 5 has 4 adjacent nodes: 1, 6, 8 and 7
• node 1 is marked as visited, so DFS continues the search by visiting the node 5
• node 6 is marked also marked as visited, so DFS continues the search by visiting the node 8
• node 8 marked as visited [so far visited: 1 ,2, 6, 5, 8], node 8 has 3 adjacent nodes: 5, 7 and 9
• node 5 is marked as visited, so DFS continues the search by visiting the node 7
• node 7 is marked as visited [so far visited: 1 ,2, 6, 5, 8, 7], node 7 has 2 adjacent nodes: node 5 and 8
• both nodes are marked as visited, so the DFS cannot go deeper, now goes back to the most recent and not marked node
• this node is the node 9, why? Node 8 was the last node that we visited and still has an adjacent node that is unmarked, the node 9
• node 9 is marked as visited [so far visited: 1 ,2, 6, 5, 8, 7, 9], node 9 has 1 adjacent node, node 8
• node 8 is marked, so we cannot continue the search deeper
• here again DFS looks for the last unmarked node
• this node is the node 3, why? Node 1 was the most recent node that still has some adjacent nodes that are unmarked, 3 and 0
• node 3 is marked as visited [so far visited: 1 ,2, 6, 5, 8, 7, 9, 3], node 3 has 1 adjacent node, node 4
• node 4 is marked as visited [so far visited: 1 ,2, 6, 5, 8, 7, 9, 3, 4], node 4 has 1 adjacent node, node 3
• node 3 is marked, so we cannot continue the search deeper
• here again DFS looks for the last unmarked node
• this node is the node 0, why?
• Node 1 was the most recent node that still has one adjacent node that is unmarked, the node 0
• node 0 is marked as visited [so far visited: 1 ,2, 6, 5, 8, 7, 9, 3, 4, 0], node 0 has 1 adjacent node, node 1
• node 1 is marked, so we cannot continue the search deeper
• here again DFS looks for the last unmarked node
• there is no such a node, which means that all nodes were visited

That was a long one :)

algorithm in plain english

What is needed for a depth first implementation:

1. a data structure to represent a graph
2. a stack (in order to go back to the most recent node that still has unvisited nodes)
3. a set that holds the already visited nodes

the algorithm in plain english:

1. initialize the graph and store it in a data structure (e.g. an adjacent list)
2. initialize an empty stack
3. initialize an empty set of visited nodes
3. select the node that you want to start the search
4. add the node in the stack
5. while there are nodes in the stack do:
6.      take/remove the first element of the stack
7.      process the data of the current node
8.      add that node in the set of the visited nodes
9.      take the adjacent nodes of the current node and
        push them in the stack (if are not marked as visited)

js implementation

the algorithm in js:

function depthFirstSearch(startNodeId, graph) {
    let visited = new Set();
    let stack = [];
    stack.push(startNodeId);

    while (stack.length !== 0) {
        currentNodeId = stack.splice(-1, 1)[0];

        // if the node is already visited continue
        if (visited.has(currentNodeId)) continue;

        // do something cool with the data
        // printing them is also cool :)
        console.log(currentNodeId);

        // add to visited nodes
        visited.add(currentNodeId);

        // get the adjacent nodes
        let adjacentNodeIds = graph[currentNodeId];

        // if not visited add them to stack
        for (let adjacentNodeId of adjacentNodeIds) {
            if (!visited.has(adjacentNodeId)) {
                stack.push(adjacentNodeId);
            }
        }
    }
}

var graph = [[1],
             [5, 0, 3, 2],
             [6, 1],
             [4, 1],
             [3],
             [7, 8, 6, 1],
             [2, 5],
             [8, 5],
             [9, 7, 5],
             [8]];

depthFirstSearch(1, graph);

Cheers!