LuckSimulations let's you play with well known gaming strategies such as martingale million of times within seconds, powered by Julia.
Think you are lucky? Do you believe 'luck favors the bold'? Think Again, This article will explain how you can you prove to yourself luck is just math - 1 roll or 100 million rolls.
Intro
LuckSimulations is a collection of Julia snippets for rapid testing and experimentation with random-number-based games such as dice, coin flip etc.
Simulations such as The infamous monty hall problem and martingale strategy in a dice game are available right now. I plan on adding more.
Implementation
LuckSimulations completely written in Julia. The reason to choose Julia is obviously, it's as fast as C and easy to write as python. The exact recipe for experiment programs which are often tweaked by users.
Design
Its a design decision to not make these functional. These are meant to snippets of code that should be run directly with required arguments directly in Terminal, any further processing(if required) can be done by user by capturing STDOUT
Monty Hall Problem:
The Monty Hall problem is a counter-intuitive statistics puzzle:
- There are 3 doors, behind which are two goats and a car.
- You pick a door (call it door A). You’re hoping for the car of course.
- Monty Hall, the game show host, examines the other doors (B & C) and opens one with a goat. (If both doors have goats, he picks randomly.)
Here’s the game: Do you stick with door A (original guess) or switch to the unopened door? Does it matter?
Surprisingly, the odds aren’t 50-50. If you switch doors you’ll win 2/3 of the time!
[source]
The Monty Hall Problem (DONG) Video
We start our code by using ArgParse to parse command line arguments provided by user.
We now store the parsed arguments into variable. Note the n_doors = 3 is part of the problem.
The main loop starts here,
3 - A array with N values i.e in our case 3 -> [0,0,0]
6 - A Door is randomly chosen to have money
7 - The door with the money values is changed to 1
9 - a door is randomly chosen as chosen_door
12 - Switch only happen if --switch arg is passed by user
17 - The host chooses to open door that does not contain money (also not the user chosen_door)
24 - The result is checked and Win/Lose is counted
30 - Result of the simulation is printed to STDOUT
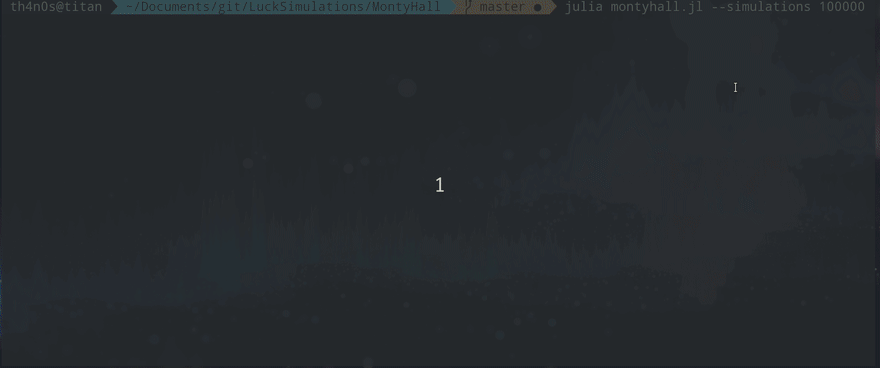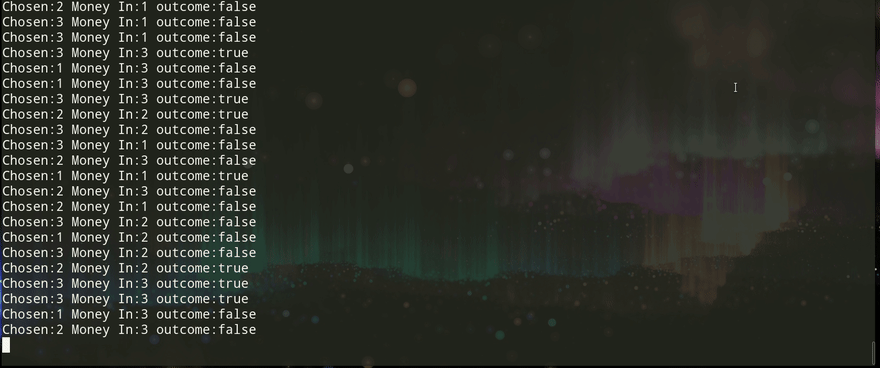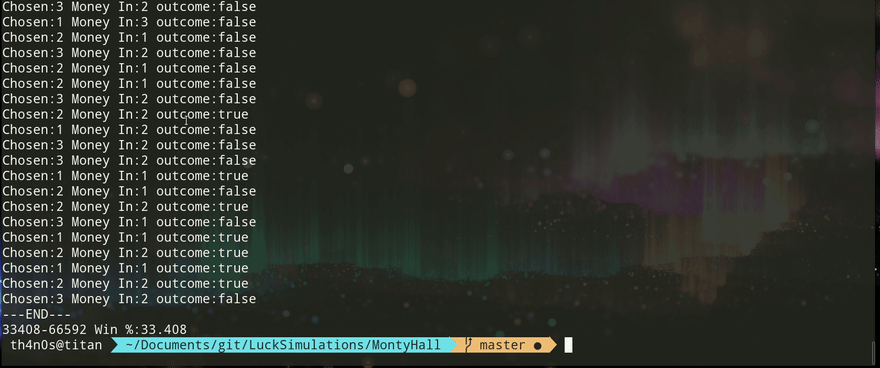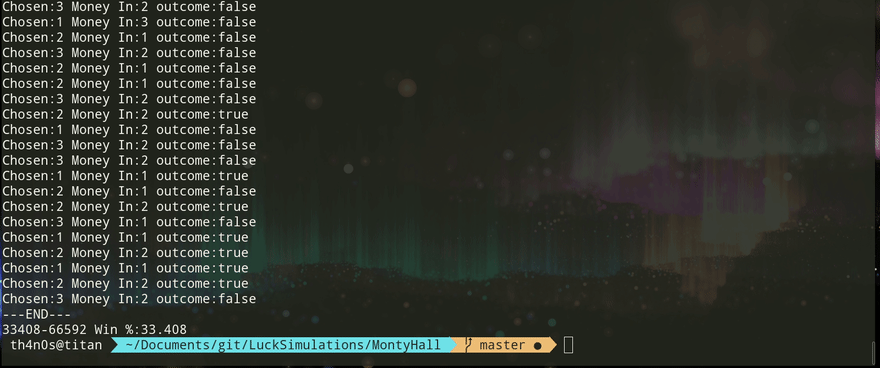
Demo
Here's a small demo how you can test this.
No Switching
Martingale Strategy in 🎲 Dice Game
A martingale is any of a class of betting strategies that originated from and were popular in 18th century France. The simplest of these strategies was designed for a game in which the gambler wins the stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double the bet after every loss, so that the first win would recover all previous losses plus win a profit equal to the original stake. The martingale strategy has been applied to roulette as well, as the probability of hitting either red or black is close to 50%.
Since a gambler with infinite wealth will, almost surely, eventually flip heads, the martingale betting strategy was seen as a sure thing by those who advocated it. None of the gamblers possessed infinite wealth, and the exponential growth of the bets would eventually bankrupt "unlucky" gamblers who chose to use the martingale. The gambler usually wins a small net reward, thus appearing to have a sound strategy. However, the gambler's expected value does indeed remain zero (or less than zero) because the small probability that the gambler will suffer a catastrophic loss exactly balances with the expected gain. (In a casino, the expected value is negative, due to the house's edge.) The likelihood of catastrophic loss may not even be very small. The bet size rises exponentially. This, combined with the fact that strings of consecutive losses actually occur more often than common intuition suggests, can bankrupt a gambler quickly.
[Source- Wiki]
Take a look at code, it should be easy to figure it out 😉
Demo
julia martingale.jl --bank 1 --stake 0.00000010 --rolls 10000000 --multiplier 2 --report-freq 10000
Hope you like this small project, Contributions are very welcome, Please open PR/Issue's.








Top comments (0)