This post is first for me, nice to meet you!
In this post, I’d like to introduce Matft library in swift to you.
Here is the source code link.
About Matft
Matft is easy and fast to operate vector, matrix, tensor(N dimensional array), and even complex and image data!
The name Matft comes from mat-rix operation library in swi-ft.
If you are accustomed to using Numpy in python, Matft will be the best option to achieve your matrix operation because Matft's function names are similar to Numpy's ones. (I'll show the examples later)
Many Numpy's functions has already implemented in Matft.
You can operate complex number as Numpy can, and there is conversion function that converts CGImage into MfArray (Matft's object of n-dimensional array) vice versa.
Also, because Matft uses the Accelerate framework (link), Matft keeps high performance (some functions even achieves higher than Numpy).
That's why I recommend to use Matft when you'd like to operate vector, matrix, tensor(N dimensional array), and even complex and image data
Basic usage
MfType
Matft's object to operate n-dimensional array is named MfArray in Matft. And MfArray has mftype property to pretend the n-dimensional array's type. (=Numpy's dtype)
Pretending means that the stored data type will be Float or Double only even if you set MfType.Int. So, if you input big number to MfArray, it may be cause to overflow or strange results in any calculation (+, -, *, /,... etc.). But I believe this is not problem in practical use.
MfType supports many types such like;
public enum MfType: Int{
case None // Unsupportted
case Bool
case UInt8
case UInt16
case UInt32
case UInt64
case UInt
case Int8
case Int16
case Int32
case Int64
case Int
case Float
case Double
case Object // Unsupported
}
Initialization
In this section, I'll show the basic initialization of MfArray.
From Swift Array
You can initialize MfArray from Swift's array. The MfType will be inferred properly.
let a = MfArray([[[ -8, -7, -6, -5],
[ -4, -3, -2, -1]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]])
print(a)
/*
mfarray =
[[[ -8, -7, -6, -5],
[ -4, -3, -2, -1]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]], type=Int, shape=[2, 2, 4]
*/
Arrange
You can create the sequence array.
let a = Matft.arange(start: -8, to: 8, by: 1, shape: [2,2,4])
print(a)
/*
mfarray =
[[[ -8, -7, -6, -5],
[ -4, -3, -2, -1]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]], type=Int, shape=[2, 2, 4]
*/
Repeated Numbers
You can create the repeated numbers array such like numpy.ones() * N.
let a = Matft.nums(Float(1), shape: [2,2,4])
print(a)
/*
mfarray =
[[[ 1.0, 1.0, 1.0, 1.0],
[ 1.0, 1.0, 1.0, 1.0]],
[[ 1.0, 1.0, 1.0, 1.0],
[ 1.0, 1.0, 1.0, 1.0]]], type=Float, shape=[2, 2, 4]
*/
Etc.
The other functions are below;
| Matft | Numpy |
|---|---|
| *#Matft.shallowcopy | *numpy.copy |
| *#Matft.deepcopy | copy.deepcopy |
| Matft.nums | numpy.ones * N |
| Matft.nums_like | numpy.ones_like * N |
| Matft.arange | numpy.arange |
| Matft.eye | numpy.eye |
| Matft.diag | numpy.diag |
| Matft.vstack | numpy.vstack |
| Matft.hstack | numpy.hstack |
| Matft.concatenate | numpy.concatenate |
| *Matft.append | numpy.append |
| *Matft.insert | numpy.insert |
| *Matft.take | numpy.take |
MfData and MfStructure Conversion
MfArray consists of two main parts, which are MfData and MfStructure.
MfData stores the pointer of raw data, the current type (=MfType), and the "stored" raw type (=StoredType, only Float or Double). On the other hand, MfStructure stores the shape and strides property, which represents the current array's structure and are same as Numpy.
So, when we exploits the MfData and MfStructure, changing the array's structure (=MfStructure) is very efficient. For example, when you have the a array initialized below;
let a = Matft.arange(start: 0, to: 27, by: 1, shape: [3,3,3])
print(a)
/*
mfarray =
[[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]]], type=Int, shape=[3, 3, 3]
*/
Type conversion
You can convert the current type into many types by astype method or function.
let a = Matft.arange(start: 0, to: 27, by: 1, shape: [3,3,3], mftype: .Int)
print(a)
/*
mfarray =
[[[ -6, -5, -4],
[ -3, -2, -1],
[ 0, 1, 2]],
[[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]],
[[ 12, 13, 14],
[ 15, 16, 17],
[ 18, 19, 20]]], type=Int, shape=[3, 3, 3]
*/
print(a.astype(.UInt8))
/*
mfarray =
[[[ 250, 251, 252],
[ 253, 254, 255],
[ 0, 1, 2]],
[[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]],
[[ 12, 13, 14],
[ 15, 16, 17],
[ 18, 19, 20]]], type=UInt8, shape=[3, 3, 3]
*/
print(a.astype(.Float))
/*
mfarray =
[[[ -6.0, -5.0, -4.0],
[ -3.0, -2.0, -1.0],
[ 0.0, 1.0, 2.0]],
[[ 3.0, 4.0, 5.0],
[ 6.0, 7.0, 8.0],
[ 9.0, 10.0, 11.0]],
[[ 12.0, 13.0, 14.0],
[ 15.0, 16.0, 17.0],
[ 18.0, 19.0, 20.0]]], type=Float, shape=[3, 3, 3]
*/
Positive and Negative Indexing
You can extract the sliced MfArrray by ~< efficiently.
Note that use a[0~<] instead of a[:] to get all elements along axis (or a[Matft.all]).
print(a[~<1]) //same as a[:1] for numpy
/*
mfarray =
[[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]]], type=Int, shape=[1, 3, 3]
*/
print(a[1~<3]) //same as a[1:3] for numpy
/*
mfarray =
[[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]]], type=Int, shape=[2, 3, 3]
*/
print(a[~<~<2]) //same as a[::2] for numpy
//print(a[~<<2]) //alias
/*
mfarray =
[[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]]], type=Int, shape=[2, 3, 3]
*/
print(a[Matft.all, 0]) //same as a[:, 0] for numpy
/*
mfarray =
[[ 0, 1, 2],
[ 9, 10, 11],
[18, 19, 20]], type=Int, shape=[3, 3]
*/
print(a[~<-1])
/*
mfarray =
[[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]]], type=Int, shape=[2, 3, 3]
*/
print(a[-1~<-3])
/*
mfarray =
[], type=Int, shape=[0, 3, 3]
*/
print(a[Matft.reverse])
//print(a[~<~<-1]) //alias
//print(a[~<<-1]) //alias
/*
mfarray =
[[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]]], type=Int, shape=[3, 3, 3]*/
Of course, you can set the value into the sliced array.
a[~<1] = Matft.arange(start: 0, to: 81, by: 9, shape: [3, 3])
print(a)
/*
mfarray =
[[[ 0, 9, 18],
[ 27, 36, 45],
[ 54, 63, 72]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]]], type=Int, shape=[3, 3, 3]
*/
Boolean Indexing
Matft supports also boolean indexing! So, you can extract the array with a specific condition you want like this. This feature will be convenient for an image processing. See the numpy docs for more details.
let img = Matft.arange(start: -5, to: 70, by: 1, shape: [5, 5, 3], mftype: .Float)
print(img)
/*
mfarray =
[[[ -5.0, -4.0, -3.0],
[ -2.0, -1.0, 0.0],
[ 1.0, 2.0, 3.0],
[ 4.0, 5.0, 6.0],
[ 7.0, 8.0, 9.0]],
[[ 10.0, 11.0, 12.0],
[ 13.0, 14.0, 15.0],
[ 16.0, 17.0, 18.0],
[ 19.0, 20.0, 21.0],
[ 22.0, 23.0, 24.0]],
[[ 25.0, 26.0, 27.0],
[ 28.0, 29.0, 30.0],
[ 31.0, 32.0, 33.0],
[ 34.0, 35.0, 36.0],
[ 37.0, 38.0, 39.0]],
[[ 40.0, 41.0, 42.0],
[ 43.0, 44.0, 45.0],
[ 46.0, 47.0, 48.0],
[ 49.0, 50.0, 51.0],
[ 52.0, 53.0, 54.0]],
[[ 55.0, 56.0, 57.0],
[ 58.0, 59.0, 60.0],
[ 61.0, 62.0, 63.0],
[ 64.0, 65.0, 66.0],
[ 67.0, 68.0, 69.0]]], type=Float, shape=[5, 5, 3]
*/
print(img[img < 0])
/*
mfarray =
[ -5.0, -4.0, -3.0, -2.0, -1.0], type=Float, shape=[5]
*/
img[img < 0] = MfArray([0])
print(img)
/*
mfarray =
[[[ 0.0, 0.0, 0.0],
[ 0.0, 0.0, 0.0],
[ 1.0, 2.0, 3.0],
[ 4.0, 5.0, 6.0],
[ 7.0, 8.0, 9.0]],
[[ 10.0, 11.0, 12.0],
[ 13.0, 14.0, 15.0],
[ 16.0, 17.0, 18.0],
[ 19.0, 20.0, 21.0],
[ 22.0, 23.0, 24.0]],
[[ 25.0, 26.0, 27.0],
[ 28.0, 29.0, 30.0],
[ 31.0, 32.0, 33.0],
[ 34.0, 35.0, 36.0],
[ 37.0, 38.0, 39.0]],
[[ 40.0, 41.0, 42.0],
[ 43.0, 44.0, 45.0],
[ 46.0, 47.0, 48.0],
[ 49.0, 50.0, 51.0],
[ 52.0, 53.0, 54.0]],
[[ 55.0, 56.0, 57.0],
[ 58.0, 59.0, 60.0],
[ 61.0, 62.0, 63.0],
[ 64.0, 65.0, 66.0],
[ 67.0, 68.0, 69.0]]], type=Float, shape=[5, 5, 3]
Fancy Indexing
Furthermore, Matft supports Fancy Indexing too! See the numpy docs for more details.
let a = MfArray([[1, 2], [3, 4], [5, 6]])
a[MfArray([0, 1, 2]), MfArray([0, -1, 0])] = MfArray([999,888,777])
print(a)
/*
mfarray =
[[ 999, 2],
[ 3, 888],
[ 777, 6]], type=Int, shape=[3, 2]
*/
a.T[MfArray([0, 1, -1]), MfArray([0, 1, 0])] = MfArray([-999,-888,-777])
print(a)
/*
mfarray =
[[ -999, -777],
[ 3, -888],
[ 777, 6]], type=Int, shape=[3, 2]
*/
Synchronizing extracted MfArray
As you can see the above examples, MfArray has base property (is similar to view in Numpy). Therefore, a MfArray extracted (Sliced) by positive and negative indexing is synchronized. See numpy doc for more details.
Note that a MfArray extracted by Boolean Indexing and Fancy Indexing is COPY of MfArray of the original one.
let a = Matft.arange(start: 0, to: 4*4*2, by: 1, shape: [4,4,2])
let b = a[0~<, 1]
b[~<<-1] = MfArray([9999])
print(a)
/*
mfarray =
[[[ 0, 1],
[ 9999, 9999],
[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[ 9999, 9999],
[ 12, 13],
[ 14, 15]],
[[ 16, 17],
[ 9999, 9999],
[ 20, 21],
[ 22, 23]],
[[ 24, 25],
[ 9999, 9999],
[ 28, 29],
[ 30, 31]]], type=Int, shape=[4, 4, 2]
*/
Etc.
The other conversion functions are below;
| Matft | Numpy |
|---|---|
| *#Matft.astype | *numpy.astype |
| *#Matft.transpose | *numpy.transpose |
| *#Matft.expand_dims | *numpy.expand_dims |
| *#Matft.squeeze | *numpy.squeeze |
| *#Matft.broadcast_to | *numpy.broadcast_to |
| *#Matft.to_contiguous | *numpy.ascontiguousarray |
| *#Matft.flatten | *numpy.flatten |
| *#Matft.flip | *numpy.flip |
| *#Matft.clip | *numpy.clip |
| *#Matft.swapaxes | *numpy.swapaxes |
| *#Matft.moveaxis | *numpy.moveaxis |
| *Matft.roll | numpy.roll |
| *Matft.sort | *numpy.sort |
| *Matft.argsort | *numpy.argsort |
| ^MfArray.toArray | ^numpy.ndarray.tolist |
| ^MfArray.toFlattenArray | n/a |
| *Matft.orderedUnique | numpy.unique |
Math operation
Basic mathematic operations are supported in Matft.
Arithmetic operation
print(a+a)
/*
mfarray =
[[ 0, 2, 4],
[ 6, 8, 10],
[ 12, 14, 16]], type=Int, shape=[3, 3]
*/
print(a-a)
/*
mfarray =
[[ 0, 0, 0],
[ 0, 0, 0],
[ 0, 0, 0]], type=Int, shape=[3, 3]
*/
print(a*a)
/*
mfarray =
[[ 0, 1, 4],
[ 9, 16, 25],
[ 36, 49, 64]], type=Int, shape=[3, 3]
*/
print(a/a)
/*
mfarray =
[[ -nan, 0.99999994, 0.99999994],
[ 0.99999994, 0.99999994, 0.99999994],
[ 0.99999994, 0.99999994, 0.99999994]], type=Float, shape=[3, 3]
*/
Broadcasting
The one of the main features in Numpy is broadcasting operation. See numpy doc for more details.
let a = Matft.arange(start: 0, to: 3*3, by: 1, shape: [3,3])
let b = MfArray([-4, 10, 2]).reshape([3, 1])
print(a+b)
/*
mfarray =
[[ -4, -3, -2],
[ 13, 14, 15],
[ 8, 9, 10]], type=Int, shape=[3, 3]
*/
Etc.
Matft has many mathematic functions.
- Math function
| Matft | Numpy |
|---|---|
| #Matft.math.sin | numpy.sin |
| Matft.math.asin | numpy.asin |
| Matft.math.sinh | numpy.sinh |
| Matft.math.asinh | numpy.asinh |
| #Matft.math.cos | numpy.cos |
| Matft.math.acos | numpy.acos |
| Matft.math.cosh | numpy.cosh |
| Matft.math.acosh | numpy.acosh |
| #Matft.math.tan | numpy.tan |
| Matft.math.atan | numpy.atan |
| Matft.math.tanh | numpy.tanh |
| Matft.math.atanh | numpy.atanh |
| Matft.math.sqrt | numpy.sqrt |
| Matft.math.rsqrt | numpy.rsqrt |
| #Matft.math.exp | numpy.exp |
| #Matft.math.log | numpy.log |
| Matft.math.log2 | numpy.log2 |
| Matft.math.log10 | numpy.log10 |
| *Matft.math.ceil | numpy.ceil |
| *Matft.math.floor | numpy.floor |
| *Matft.math.trunc | numpy.trunc |
| *Matft.math.nearest | numpy.nearest |
| *Matft.math.round | numpy.round |
| #Matft.math.abs | numpy.abs |
| Matft.math.reciprocal | numpy.reciprocal |
| #Matft.math.power | numpy.power |
| Matft.math.arctan2 | numpy.arctan2 |
| Matft.math.square | numpy.square |
| Matft.math.sign | numpy.sign |
- Statistics function
| Matft | Numpy |
|---|---|
| *Matft.stats.mean | *numpy.mean |
| *Matft.stats.max | *numpy.max |
| *Matft.stats.argmax | *numpy.argmax |
| *Matft.stats.min | *numpy.min |
| *Matft.stats.argmin | *numpy.argmin |
| *Matft.stats.sum | *numpy.sum |
| Matft.stats.maximum | numpy.maximum |
| Matft.stats.minimum | numpy.minimum |
| *Matft.stats.sumsqrt | n/a |
| *Matft.stats.squaresum | n/a |
| *Matft.stats.cumsum | *numpy.cumsum |
- Random function
| Matft | Numpy |
|---|---|
| Matft.random.rand | numpy.random.rand |
| Matft.random.randint | numpy.random.randint |
- Linear algebra
| Matft | Numpy |
|---|---|
| Matft.linalg.solve | numpy.linalg.solve |
| Matft.linalg.inv | numpy.linalg.inv |
| Matft.linalg.det | numpy.linalg.det |
| Matft.linalg.eigen | numpy.linalg.eig |
| Matft.linalg.svd | numpy.linalg.svd |
| Matft.linalg.pinv | numpy.linalg.pinv |
| Matft.linalg.polar_left | scipy.linalg.polar |
| Matft.linalg.polar_right | scipy.linalg.polar |
| Matft.linalg.normlp_vec | scipy.linalg.norm |
| Matft.linalg.normfro_mat | scipy.linalg.norm |
| Matft.linalg.normnuc_mat | scipy.linalg.norm |
Advanced operation
Matft has complex and image processing functions too!!!!
So, Matft will be very useful for the signal and image processing!
But these functions are beta versions currently (on 22/08/08).
Complex operation
You can operate the complex values like the real ones.
let real = Matft.arange(start: 0, to: 16, by: 1).reshape([2,2,4])
let imag = Matft.arange(start: 0, to: -16, by: -1).reshape([2,2,4])
let a = MfArray(real: real, imag: imag)
print(a)
/*
mfarray =
[[[ 0 +0j, 1 -1j, 2 -2j, 3 -3j],
[ 4 -4j, 5 -5j, 6 -6j, 7 -7j]],
[[ 8 -8j, 9 -9j, 10 -10j, 11 -11j],
[ 12 -12j, 13 -13j, 14 -14j, 15 -15j]]], type=Int, shape=[2, 2, 4]
*/
print(a+a)
/*
mfarray =
[[[ 0 +0j, 2 -2j, 4 -4j, 6 -6j],
[ 8 -8j, 10 -10j, 12 -12j, 14 -14j]],
[[ 16 -16j, 18 -18j, 20 -20j, 22 -22j],
[ 24 -24j, 26 -26j, 28 -28j, 30 -30j]]], type=Int, shape=[2, 2, 4]
*/
print(Matft.complex.angle(a))
/*
mfarray =
[[[ -0.0, -0.7853982, -0.7853982, -0.7853982],
[ -0.7853982, -0.7853982, -0.7853982, -0.7853982]],
[[ -0.7853982, -0.7853982, -0.7853982, -0.7853982],
[ -0.7853982, -0.7853982, -0.7853982, -0.7853982]]], type=Float, shape=[2, 2, 4]
*/
print(Matft.complex.conjugate(a))
/*
mfarray =
[[[ 0 +0j, 1 +1j, 2 +2j, 3 +3j],
[ 4 +4j, 5 +5j, 6 +6j, 7 +7j]],
[[ 8 +8j, 9 +9j, 10 +10j, 11 +11j],
[ 12 +12j, 13 +13j, 14 +14j, 15 +15j]]], type=Int, shape=[2, 2, 4]
*/
| Matft | Numpy |
|---|---|
| Matft.complex.angle | numpy.angle |
| Matft.complex.conjugate | numpy.conj / numpy.conjugate |
| Matft.complex.abs | numpy.abs / numpy.absolute |
Image operation
Conversion from/to CGImage
The conversion functions between MfArray and CGImage are ready. So, you can implement the complex image operation code
very easily! For example, if you use the Matft's indexing feature,...
import UIKit
import Matft
import Accelerate
import CoreGraphics
import CoreGraphics.CGBitmapContext
class ViewController: UIViewController {
@IBOutlet weak var originalImageView: UIImageView!
@IBOutlet weak var reverseImageView: UIImageView!
@IBOutlet weak var grayreverseImageView: UIImageView!
@IBOutlet weak var swapImageView: UIImageView!
override func viewDidLoad() {
super.viewDidLoad()
self.originalImageView.image = UIImage(named: "rena.jpeg")
self.reverseImageView.image = UIImage(named: "rena.jpeg")
self.grayreverseImageView.image = self.convertToGrayScale(image: UIImage(named: "rena.jpeg")!)
self.swapImageView.image = UIImage(named: "rena.jpeg")
self.reverse()
self.grayreverse()
self.swapchannel()
self.resize()
}
func reverse(){
var image = Matft.image.cgimage2mfarray(self.reverseImageView.image!.cgImage!)
// reverse
image = image[Matft.reverse] // same as image[~<<-1]
self.reverseImageView.image = UIImage(cgImage: Matft.image.mfarray2cgimage(image))
}
func swapchannel(){
var image = Matft.image.cgimage2mfarray(self.swapImageView.image!.cgImage!)
// swap channel
image = image[Matft.all, Matft.all, MfArray([1,0,2,3])] // same as image[0~<, 0~<, MfArray([1,0,2,3])]
self.swapImageView.image = UIImage(cgImage: Matft.image.mfarray2cgimage(image))
}
func grayreverse(){
var image = Matft.image.cgimage2mfarray(self.grayreverseImageView.image!.cgImage!, mftype: .UInt8)
// reverse
image = image[Matft.reverse] // same as image[~<<-1]
self.grayreverseImageView.image = UIImage(cgImage: Matft.image.mfarray2cgimage(image))
}
func convertToGrayScale(image: UIImage) -> UIImage{
//let gray_mfarray = (Matft.image.color(Matft.image.cgimage2mfarray(image.cgImage!)) * Float(255)).astype(.UInt8)
let gray_mfarray = Matft.image.color(Matft.image.cgimage2mfarray(image.cgImage!))
return UIImage(cgImage: Matft.image.mfarray2cgimage(gray_mfarray))
}
func resize(){
var image = Matft.image.cgimage2mfarray(self.swapImageView.image!.cgImage!)
// resize
image = Matft.image.resize(image, width: 300, height: 300)
self.swapImageView.image = UIImage(cgImage: Matft.image.mfarray2cgimage(image))
//self.swapImageView.frame = CGRect(x: 0, y: 0, width: 300, height: 300)
}
}
Awesome!
Affine
// CGImage to MfArray
let rgb = Matft.image.cgimage2mfarray(uiimage.cgImage!)
// Convert RGBA into Gray Image
let gray = Matft.image.color(rgb)
// Resize
let rgb_resize = Matft.image.resize(rgb, width: 150, height: 150)
let gray_resize = Matft.image.resize(gray, width: 300, height: 300)
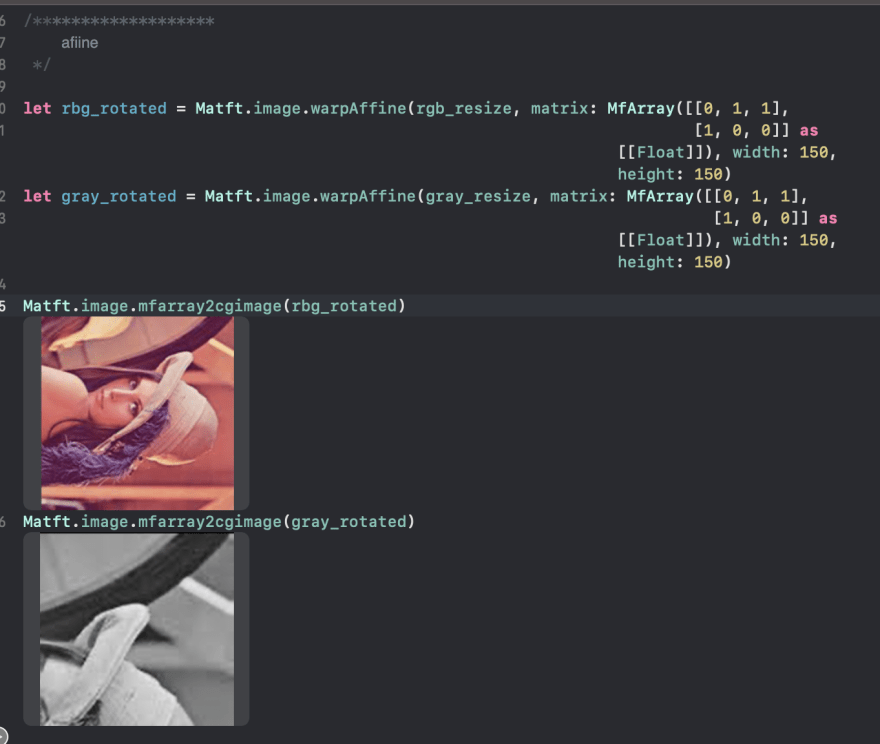
let rbg_rotated = Matft.image.warpAffine(rgb_resize, matrix: MfArray([[0, 1, 1],
[1, 0, 0]] as [[Float]]), width: 150, height: 150)
let gray_rotated = Matft.image.warpAffine(gray_resize, matrix: MfArray([[0, 1, 1],
[1, 0, 0]] as [[Float]]), width: 150, height: 150)
Matft.image.mfarray2cgimage(rbg_rotated)
| Matft | Numpy |
|---|---|
| Matft.image.cgimage2mfarray | N/A |
| Matft.image.mfarray2cgimage | N/A |
| Matft | OpenCV |
|---|---|
| Matft.image.color | cv2.cvtColor |
| Matft.image.resize | cv2.resize |
| Matft.image.warpAffine | cv2.warpAffine |
Conclusion
I introduced the Matft in this post. Matft has many features from the basic mathematic array operations to the complicated operations such like boolean indexing, fancy indexing, complex data, image data and so on.
I hope Matft will be useful for your project and help your project more efficient!



Top comments (0)