My summary of Leet Code [Binary Tree explore card](https://leetcode.com/explore/learn/card/data-structure-tree Also using GeeksforGeeks Binary Tree articles
Tree
Each node of tree has root value and list of references to other nodes (called child nodes)
From a graph point of view
directed acyclic graph which has N nodes and N-1 edges.
Binary Tree
tree structure where each node has at most two children. (left child & right child)
Traversing a Tree
- Pre-order (root, left, right)
- In-order (left, root, right)
- Post-order (left, right, root)
- level-order traversal
This article provides a great overview of tree traversals and how they relate to BFS / DFS
1. Pre-Order Traversal
- visit root
- visit left sub tree
- visit right sub tree
(root first, then left right children)


Applications
- used to create copy of a tree.
- get prefix expression of an expression tree. (e.g. Polish notation)
class Solution{
ArrayList<Integer> result = new ArrayList<>();
ArrayList<Integer> preorder(Node root) {
if (root != null) {
result.add(root.data);
}
if (root != null && root.left != null) {
result.add(root.left);
}
if (root != null && root.right != null) {
result.add(root.right);
}
return result;
}
}
2. Post-order Traversal
- visit left sub tree
- visit right sub tree
- visit root
(children left,right first, then root)

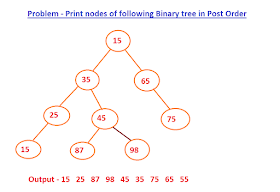
Applications
- delete tree
- get postfix expressions (e.g. reverse polish notation)
class Tree {
ArrayList<Integer> result = new ArrayList<>();
ArrayList<Integer> postOrder(Node root) {
if (root != null && root.left!=null) {
postOrder(root.left);
}
if (root != null && root.right!= null) {
postOrder(root.right);
}
if (root != null) {
result.add(root.data);
}
return result;
}
}
3. In-order Traversal
- visit left subtree
- visit root
- visit right subtree
(left -> right, left root right)
Applications
- in BST, inorder traversal gives nodes in non-decreasing order.
class Solution {
ArrayList<Integer> result = new ArrayList<>();
ArrayList<Integer> inOrder(Node root)
{
if (root != null && root.left!= null) {
inOrder(root.left);
}
if (root != null) {
result.add(root.data);
}
if (root != null && root.right!=null) {
inOrder(root.right);
}
return result;
}
}
4. Level order tarversal
traverse tree by level
- visit root node
- visit children of root node
- visit children of children of root node
- continue till leaf nodes
Applications
- BFS
Traversal - Complexity
Time complexity: O(1)
Space Complexity: (consider size of stack for function calls)
Worst: O(N) (skewed tree)
Best: O(log(n)) (balanced tree)
Properties
1. maximum number of nodes at height h is 2h
level of root = 0
For root, h=0 and number of nodes is 20 = 1
Therefore number of nodes when h = h is 2h
2. Maximum number of nodes in a BINARY tree of height h is 2h – 1.
In binary tree node can only have at most two children.
keep in mind that height index of root is 0. But height h refers to the number of nodes from root to leaf. Therefore leaf nodes have height index of h-1. (something like array indexes VS array length)
So total number of nodes in tree is
= 20 + 21 + 22 + ... + 2h-1
= 1 + 2 + 4 + ... + 2h-1
= 2 h - 1 (geometric series)
Mathematical proof for last line:

3. In BINARY tree with N nodes, minimum possible height is log2(N+1).
Using point above we know that
2h - 1 = N
2h = N + 1
h = log2(N+1)
In Big O notation this is usually expressed as O(log(n))
4. BINARY Tree with L leaves has at least |log2L|+ 1 levels
From point 1 we know that the number of leaf nodes are 2h-1.
2h-1 = L
log2L = h - 1
h = log2(L) + 1
5. In a full binary tree, the number of leaf nodes is always one more than nodes with two children.
more here
Binary Tree Types
- Full Binary Tree
- Complete Binary Tree
- Perfect Binary Tree
- Balanced Binary Tree
- Degenerate / pathological tree
This article gives a good description of each type of binary trees. and this article gives good illustrations of valid/ invalid types of binary treees.
1. Full Binary Tree
every node has either 0 or 2 children

Here the number of leaf nodes (no children) = number of internal nodes (2 children) + 1
2. Complete Binary Tree
All the levels are completely filled except the last level (level of height h) & last level has all keys as left as possible
3. Perfect Binary Tree
all the internal nodes have two children and all leaf nodes are at the same level.
Here, number of leaf nodes = number of internal nodes + 1.
In perfect binary tree, number of nodes is maximum number of nodes 2h +1
4. Balanced Binary Tree
Binary tree that is height balanced
left and right subtrees of every node differ in height by no more than 1.
- left and right subtrees' heights differ by at most one, AND
- The left subtree is balanced, AND
- The right subtree is balanced

In balanced tree, height is O(log(n))
5. Degenerate / pathological tree
every parent node has 1 child
- behaves like linked list
- height is n
- worst case complexity basically super cursed

Binary Search Tree
Summary from LeetCode Explore Card
Its a binary tree satisfying binary search property
special form of binary tree where: value in is node must be
greater than (or equal to) any values in its left subtree AND
less than (or equal to) any values in its right subtree.
Traversal
same as binary tree only that:
inorder traversal = ascending order
Search
For each node:
- if target value == node vale return the node
- if target value < node value search in left subtree
- if target value > node value search in right subtree
Search - Recursive
public TreeNode searchBST(TreeNode root, int val) {
if (root == null) {
return null;
} else {
if (root.val == val) {
return root;
} else if ( root.val > val ) {
return searchBST(root.left, val);
} else {
// root.val < val
return searchBST(root.right, val);
}
}
}
Time Complexity
time complexity is O(h) where h is height of binary tree
Height Balanced: O(log(n))
Height Skewed: O(n) (n is the number of nodes in tree)
Space Complexity
More details in stack overflow answer
Space complexity of tree: O(n)
Space complexity of recursive function is the height of the stack which would be the height of the binary tree.
Height Balanced: O(log(n))
Height Skewed: O(n)
Search - Iterative
public TreeNode searchBST(TreeNode root, int val) {
TreeNode init = root;
while (init != null) {
if (init.val == val) {
return init;
} else if (init.val > val) {
init = init.left;
} else {
init = init.right;
}
}
return init;
}
Time Complexity
Height Balanced: O(log(n))
Height Skewed: O(n)
Space Complexity
space complexity of tree: O(n)
Auxillary space complexity: O(1)
Insert
Find proper leaf position for target node and insert node as a leaf.
- search left or right subtrees (if node.value > target or node.value < target)
- repeat step1 until reach a leaf node
- add new node as its left / right child
Insert - Recursive
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
} else {
return insert(root, root, val);
}
}
public TreeNode insert(TreeNode root, TreeNode current, int val) {
if (current.val < val && current.right != null) {
return insert(root, current.right, val);
} else if (current.val < val && current.right == null) {
current.right = new TreeNode(val);
return root;
} else if (current.val > val && current.left !=null) {
return insert(root, current.left, val);
} else { // root.val > vall && root.left==null
current.left = new TreeNode(val);
return root;
}
}
Time Complexity
Time complexity will be proportional to height.
Height Balanced: O(log(n))
Height Skewed: O(n)
Auxillary Space Complexity
Height of recursion stack ~ height of BST
Height balanced: O(log(n))
Height Skewed: O(n)
Insert - Iterative
Node insert(Node root, int Key) {
Node init = root;
while (true) {
if (init.data == Key) {
break;
} else {
if (init.data < Key) {
if (init.right != null) {
init = init.right;
} else {
// init.right == null
init.right = new Node(Key);
break;
}
} else {
// init.val > Key
if (init.left != null) {
init = init.left;
} else {
init.left = new Node(Key);
break;
}
}
}
}
return root;
}
Time Complexity
Traversing BST. proportional to height of BST
Height Balanced: O(log(n))
Height Skewed: O(n)
Auxillary Space Complexity
Store current node. constant space
Complexity: O(1)
Deletion
- target node has no child: remove the node.
- target node has one child: use child to replace itself.
- target node has two children: replace the node with its in-order successor / predecessor & and delete target node.
In-order successor: smallest node in right subtree
In-Order predecessor: biggest node in left subtree
class Tree {
// Return the root of the modified BST after deleting the node with value X
public static Node deleteNode(Node root, int X){
// code here.
Node pre = null;
Node toDelete = root;
while (toDelete != null && toDelete.data != X) {
pre = toDelete;
if (toDelete.data < X) {
toDelete = toDelete.right;
} else {
toDelete = toDelete.left;
}
}
if (toDelete == null) {
// node not found
return root;
} else {
// delete node
if (toDelete.left == null && toDelete.right ==null) {
// no children
if (pre == null) {
return null;
} else {
if (pre.left == toDelete) {
pre.left = null;
} else {
pre.right = null;
}
}
} else if (toDelete.left != null && toDelete.right != null) {
// two children
// inorder successor (smallest number in right subtree)
Node preSucc = toDelete;
Node successor = toDelete.right;
while (successor.left != null) {
preSucc = successor;
successor = successor.left;
}
toDelete.data = successor.data;
if (preSucc.left == successor) {
preSucc.left = null;
} else {
preSucc.right = null;
}
} else {
// onyl 1 child
Node child = null;
if (toDelete.left == null) {
child = toDelete.right;
} else {
child = toDelete.left;
}
if (pre.left == toDelete) {
pre.left = child;
} else {
pre.right = child;
}
}
}
return root;
}
}
Self-balancing Binary tree
1. AVL Tree
left subtree & right subtree height diff <= 1
After insert, if height difference > 1, rotations are performed to balance tree
2. Red-Black Tree
- each node painted red or black.
- root of tree is always black
- red node cannot have red parent or red child
- every path from node (incl. root) to any of the NULL nodes have same number of black nodes
balances by ensuring that a chai of 3 nodes never gets to form.
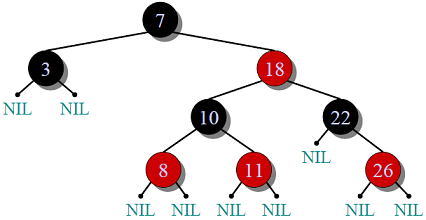
Info from: SO
- AVL more rigidly balanced -> provide faster look ups
- Insert intensive tasks -> red-black
- AVL may take more space. AVL store balance factor at each node (O(n)) space. for red-black if data stored in all nodes is >0. sign bit store colour information
Red-black is used for Java TreeMap & TreeSet
Heap
Binary Heap
- min-heap
- max-heap
min / max -heap is complete binary tree where value of root node is <= / >= either of its children. Same property must be recursively true for all subtrees in binary tree.
Analysis
- use when ordering is important (e.g. priority queue)
- good at doing comparative operations e.g. if you want values above x. just grab all parents of node X. no need to do any traversals all the down to leaf nodes.
Lookup
unlike BST, left and right subtree has no meaning. you can't divide the tree to search it.
Must go through all nodes
Complexity: O(n)
deletion: O(log(n))
Insertion:
- increase heap size by 1
- insert new element at end of heap
-
Heapify. let last node "bubbles up" (swaps with parents)
Complexity:
O(log(n))unlike BST, left and right subtree has no meaning. you can't divide the tree to search it.
deletion
- replace root / element by last element
- delete last element from Heap
- heapify to ensure last node is in correct position
Analysis
- insertion is better tha O(n)
- priority
- flexible size
- slow lookup. (fast if its finding max or min)
Priority Queue
Queue is FIFO. Objects with higher priority that enter later and get out first.
- every element has priority associated with it
- element with high priority is dequeued befor an element with low priority
- 2 elements have same priority they are served according to order in queue.

e.g. emergency room
Heap can be represented in the form of an array. In binary heap priority queue, objects with higher priority would be higher up.
Then look at binary heap as an array and dequeue objects.
Trie / Prefix tree
specialized tree for searching text.
can have >2 children. use to search if character in word exists / subword in word exists.
Space advantage: since its a prefix tree, if words share same prefix, dont have to store it twice.
Search
Lookup for word. Look up for first character. then search children to see if other characters match.
Complexity is the height of the tree.
Complexity: O(log(n))
Insertion
if character doesnt exist need to create new children. If character exists, mark end of word for last node.
insertion requires one to go down depth of trie.
Complexity: O(log(n))
Reasons for using Trees
- Store information that naturally forms hierarchy. Eg. the file system on a computer.
- Trees (e.g. BST) may provide moderately quick access/search. Quicker than Linked List, slower than arrays.
- Trees provide moderate insertion/deletion, Quicker than arrays, slower than unordered linked lists.
- No limit on number of nodes since nodes are linked using pointers (like linked list, unlike arrays)













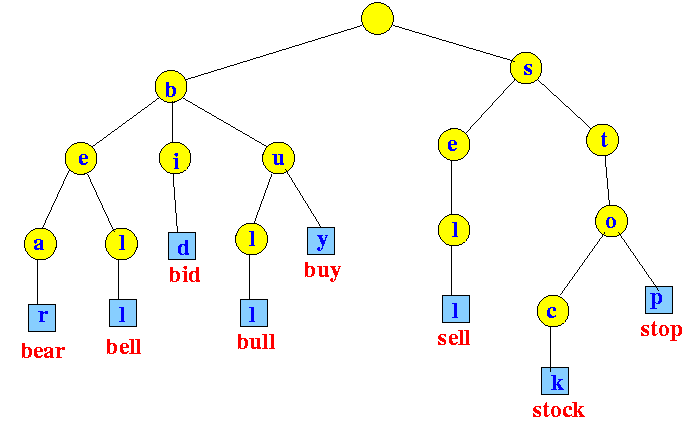





Top comments (0)