I thought of compiling together some of the common Data Structures and Algorithms implementations in Javascript and sharing them with the community. This is Part 1 of the series.
This article is intended as a starting point for someone who is prepping for a DS and Algorithms job interview.
In Part 1, we will cover
- Stack
- Queue
- Binary Search Tree
Part 2 covers Merge Sort and Binary Search.
Part 3 covers the solutions for finding the most frequently occurring item in an array, Sum of elements of a nested array and Array chunks.
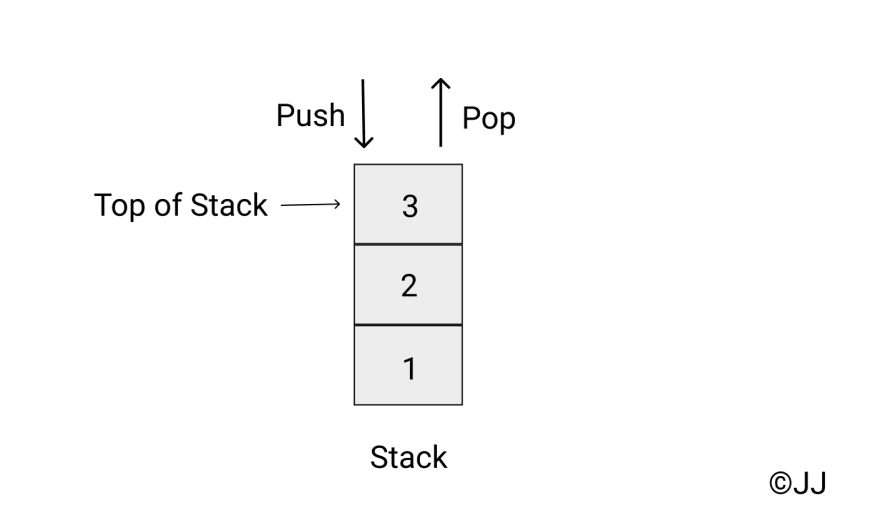
1. Stack
Stack is a linear data structure that follows LIFO (Last In First Out) or FILO (First In Last Out). There are two main operations on a Stack.
- Push - adds an element to the top of the Stack.
- Pop - removes the most recently added element (from the top of the Stack).
class Node {
constructor(value) {
this.value = value;
this.prev = null;
}
}
class Stack {
constructor() {
this.top = null; // no nodes
}
push(value) {
let node = new Node(value);
node.prev = this.top;
this.top = node;
}
pop() {
if (this.top) {
let value = this.top.value;
this.top = this.top.prev;
return value;
} else {
return 'Stack is empty';
}
}
}
let stack1 = new Stack(); // stack to store integers
stack1.push(1);
stack1.push(2);
stack1.push(3);
console.log(stack1.pop()); // 3
console.log(stack1.pop()); // 2
console.log(stack1.pop()); // 1
console.log(stack1.pop()); // stack is empty
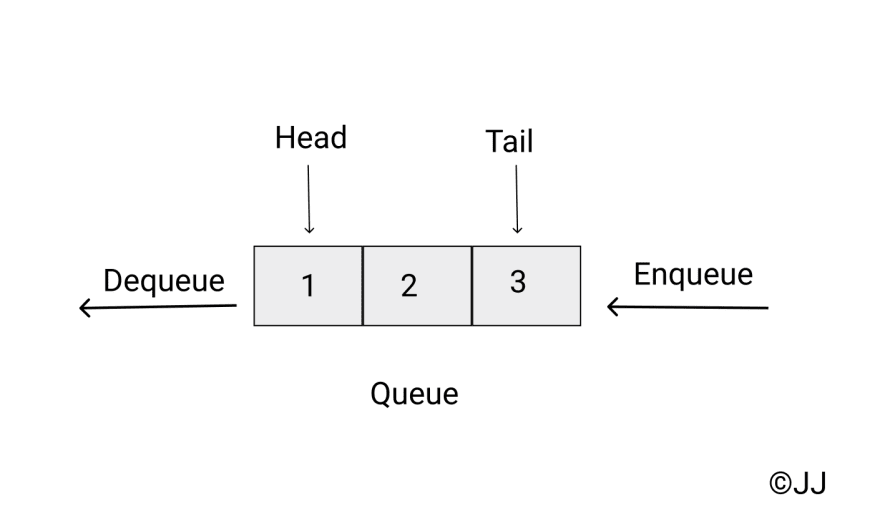
2. Queue
Queue is also a linear data structure. Queue follows FIFO (First In First Out). The two main operations on Queue are:
- Enqueue - adds an element to the tail of the Queue.
- Dequeue - removes an element from the head of the Queue.
class Node {
constructor(val) {
this.value = val;
this.next = null;
}
}
class Queue {
constructor() {
this.head = null;
this.tail = null;
}
enqueue(val) {
// to tail
let node = new Node(val);
if (!this.head) {
//if queue is empty, point head and tail to this new node
this.head = this.tail = node;
} else {
this.tail.next = node;
this.tail = node; // make new node as tail
}
}
dequeue() {
// from head
if (this.head) {
let val = this.head.value;
this.head = this.head.next;
return val;
} else {
return 'Queue is empty';
}
}
}
let q1 = new Queue();
q1.enqueue(1);
q1.enqueue(2);
q1.enqueue(3);
console.log(q1.dequeue()); // 1
console.log(q1.dequeue()); // 2
console.log(q1.dequeue()); // 3
console.log(q1.dequeue()); // Queue is empty
3. Binary Search Tree
A Binary Search Tree is an ordered or sorted binary tree.
- There is a root node
- Each node (including the root node) has a key greater than all the keys in the node's left subtree and less than those in its right subtree
Insertion
- The key of the new node is first compared with that of the root.
- If the key of the new node is less than the root's, then the new node is compared with the key of the root's left child.
- If the key of the new node is greater than the root's, then the new node is compared with the root's right child.
- This process continues until the new node is compared with a leaf node, and then it is added as this node's right or left child, depending on its key. If the key is less than the leaf's key, then it is inserted as the leaf's left child, otherwise as the leaf's right child.
Traversal
There are 3 common binary tree traversals.
- Pre-order (Node->Left->Right)
- In-order (Left->Node->Right)
- Post-order (Left->Right->Node)
An in-order traversal of a binary search tree will always result in an ascending sorted list of node items. Here, I have implemented in-order traversal.
- Traverse the left subtree by recursively calling the printNode function.
- Print the key of the current node.
- Traverse the right subtree by recursively calling the printNode function.
class Node {
constructor(val) {
this.value = val;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null; // root node
}
insertNode(parentNode, newNode) {
if (newNode.value < parentNode.value) {
//check the left child
parentNode.left !== null
? this.insertNode(parentNode.left, newNode)
: (parentNode.left = newNode);
} else {
// check the right child
parentNode.right !== null
? this.insertNode(parentNode.right, newNode)
: (parentNode.right = newNode);
}
}
insert(val) {
let newNode = new Node(val);
this.root !== null
? this.insertNode(this.root, newNode)
: (this.root = newNode);
}
printNode(node) {
if (node.left !== null) {
this.printNode(node.left); // traverse left subtree
}
console.log(node.value);
if (node.right !== null) {
this.printNode(node.right); // traverse right subtree
}
}
print() {
this.root !== null
? this.printNode(this.root)
: console.log('No nodes in the tree');
}
}
let bst1 = new BinarySearchTree();
bst1.insert(50);
bst1.insert(30);
bst1.insert(10);
bst1.insert(40);
bst1.insert(20);
bst1.insert(80);
bst1.insert(70);
bst1.insert(60);
bst1.insert(100);
bst1.insert(90);
bst1.print();
Hope this helps!
Don't forget to checkout Part 2 and Part 3 of this series.
More coming soon!!




Top comments (0)