ECDSA in Bitcoin

Here is this article in short video form:
https://www.youtube.com/watch?v=tl6RGKKvHto

Since I never took computer science courses, I have to catch up with some of the fundamentals, and I find them fascinating. One such fundamental of computer science is cryptography, and today I want to go through how it is applied to generate wallets in Bitcoin from scratch.

The math used to generate a wallet from scratch is called Elliptic Curve Cryptography. It used in Bitcoin and is crucial to maintaining the integrity of the protocol. The amazing part is that it is so secure, that you don't have to even be connected to the internet because this process is just based on math.

Let’s get into how it works.

Everything is based on this curve called the Secp256k1 derived by the function

y = sqrt(x**3 + 7)

To use it, we generate any random number up to 2^256 and multiply it by a constant point G in the curve

The point G is constant for every bitcoin address and here it is as x and y coordinates:

The math that is more interesting and we are more concerned about is how to generate a public key from ANY random number. And that math is a simple function here:

K = k  * G

where k is the private key, G is a constant point called the generator point, and K is the resulting public key.

k can be anything, the important part is that it is random. Once you have a random value for k you just multiply that by G which is the process of extending a tangent until it intersects with a different point in the line and reflecting that point across the X axis.

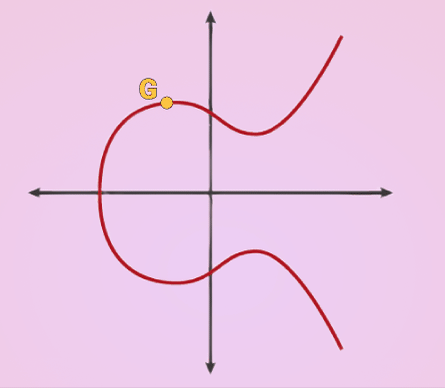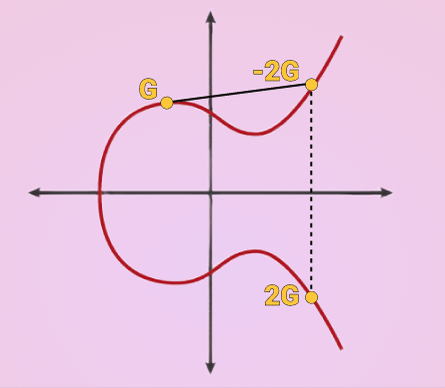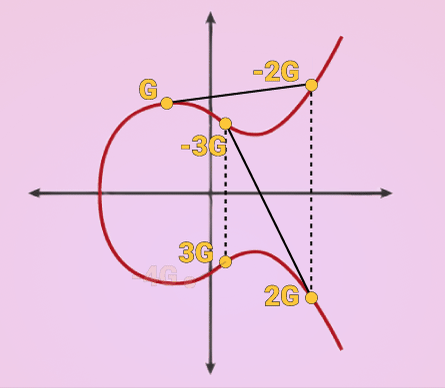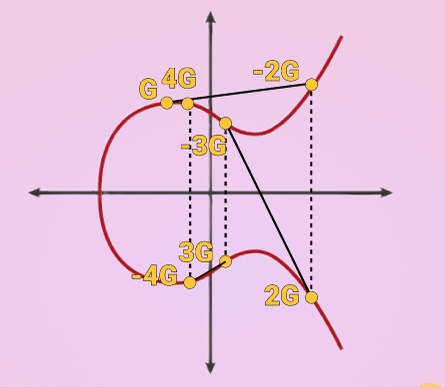
The result is called your public key and can be shared with ANYONE because it is extremely improbable that someone can derive the private key backwards from it.

You still have to run it through some hashing functions to generate an address, but this is pretty much it. This math has been around since the 80s and is considered secure enough to hide government secrets. By signing a transaction with that private key, you are basically proving that you are the only person with access to the private key used to generate that public key.