Using funmark to benchmark python function and plot results

Before starting the blog I wanted to say that this is my first PyPI package and it is still in the development phase so if anyone finds it interesting, make sure to checkout funmark in GitHub

Funmark is a python package that can be used for function benchmarking and then to analyze/compare their runtime and memory consumption using graph plots.

In this blog I will be using my funmark package to benchmark sorting functions, mainly

• QuickSort
• MergeSort
• TimSort

Let's Start by first importing funmark and random.randint() for creating random arrays

import funmark
from random import randint

Let's create functions for each sorting method

QuickSort

def partition(arr,low,high): 
    i = ( low-1 )         # index of smaller element 
    pivot = arr[high]     # pivot 
    for j in range(low , high): 
        if   arr[j] < pivot: 
            i = i+1 
            arr[i],arr[j] = arr[j],arr[i] 

    arr[i+1],arr[high] = arr[high],arr[i+1] 
    return ( i+1 ) 

def quickSort(argv): 
    arr = argv[0]
    low = argv[1]
    high = argv[2]
    if low < high: 
        pi = partition(arr,low,high) 
        quickSort([arr, low, pi-1]) 
        quickSort([arr, pi+1, high]) 

MergeSort

def mergeList(arr, l, m, r): 
    n1 = m - l + 1
    n2 = r- m 
    L = [0] * (n1) 
    R = [0] * (n2) 
    for i in range(0 , n1): 
        L[i] = arr[l + i] 
    for j in range(0 , n2): 
        R[j] = arr[m + 1 + j] 
    i = 0     
    j = 0 
    k = l     
    while i < n1 and j < n2 : 
        if L[i] <= R[j]: 
            arr[k] = L[i] 
            i += 1
        else: 
            arr[k] = R[j] 
            j += 1
        k += 1
    while i < n1: 
        arr[k] = L[i] 
        i += 1
        k += 1
    while j < n2: 
        arr[k] = R[j] 
        j += 1
        k += 1

def mergeSort(argv):
    arr = argv[0]
    l = argv[1]
    r = argv[2]
    if l < r: 
        m = (l+(r-1))//2 
        mergeSort([arr, l, m]) 
        mergeSort([arr, m+1, r]) 
        mergeList(arr, l, m, r) 

TimSort

def timSort(argv):
    ar = argv[0]
    ar.sort()
    return ar

BenchMarking the above functions

Lets create funmark.Benchmark() objects for each functions

merge = funmark.Benchmark()
quick = funmark.Benchmark()
tim = funmark.Benchmark()

Now lets create random arrays of sizes ranging from

listSize = 10
maxSize = 10**6
while listSize < maxSize:
    ar = [randint(1,10**5) for listSize in range(listSize)]

    time, memory = merge.run(quickSort, ar, 0, len(ar)-1)
    merge.add(len(ar), time, memory)

    time, memory= quick.run(mergeSort, ar, 0, len(ar)-1)
    quick.add(len(ar), time, memory)

    time, memory = tim.run(timSort, ar)
    tim.add(len(ar), time, memory)

    listSize = int(2*listSize)

For each function, I am running .run(function Name, parameter) to get their runtime and memory usage, and then I am saving them to their respective objects using .add(size, time, memory)
At the last line of while loop and increasing the size of listSize so that we can get these values for different sizes of the list

Plotting comparison graphs

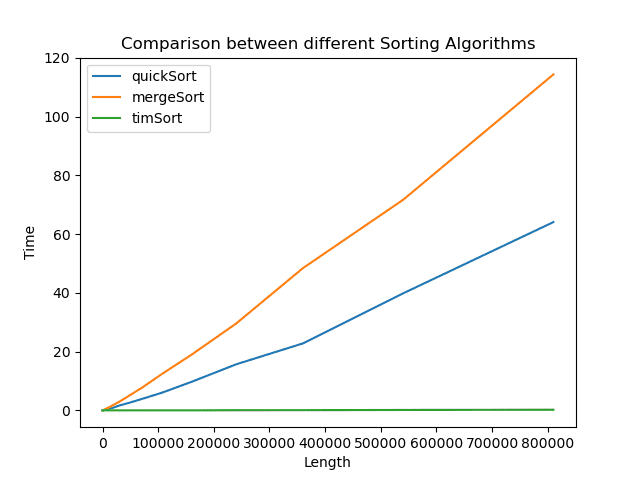
merge.compareTime("Length", "Time", "Compression between Sorting Algorithms", quick, tim)

Here I am plotting the graph of time with merge and passing quick and tim to plot all of them together, here is the result of this line

As you can see QuickSort even though has bigger worst case time complexity that MergeSort, its average case is much better due to

• Auxiliary Space: Quicksort is an in-place sorting algorithm. Merge sort on the other hand requires a temporary array to merge the sorted arrays and hence it is not in-place.

• Worst case: The worst case of quicksort O(n^2) can be avoided by using randomized quicksort. It can be easily avoided with high probability by choosing the right pivot.

• Locality of reference: Quicksort in particular exhibits good cache locality and this makes it faster than merge sort in many cases like in a virtual memory environment.

• Tail recursion: QuickSort is tail recursive while Merge sort is not. A tail recursive function is a function where a recursive call is the last thing executed by the function. They are considered better than non tail recursive functions as they can be optimized by the compiler before execution.

And Tim Sort performs exceptionally better than both as expected, hence it's better to use python's in-build .sort() method as long as your need is plain sorting.

merge.compareMemory("Length", "Time", "Compression between Sorting Algorithms", quick, tim)

Here I am plotting the graph of memory with mergeSort and passing quickSort and timSort to plot all of them together, here is the result of this line

The plot for QuickSort is just below the TimSort plot hence it isn't clearly visible in this plot but from this we can understand that MergeSort requires extra space whereas QuickSort and TimSort don't!

This was just a simple analysis of Sorting Algorithms but funmark can be used to do benchmark and analysis for any python code as long as it can be written in a function.

If you liked what this library can do then check it out on github and drop a star and look into the issue tab if you want to contribute!