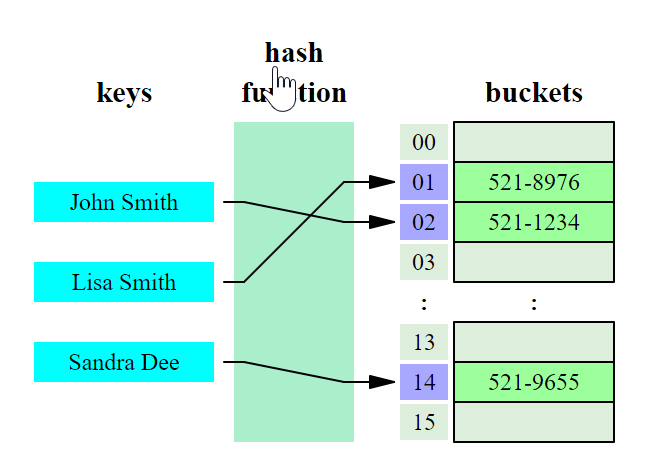
In computing, a hash table (hash map) is a data structure that implements an associative array abstract data type, a structure that can map keys to values. A hash table uses a hash function to compute an index into an array of buckets or slots, from which the desired value can be found
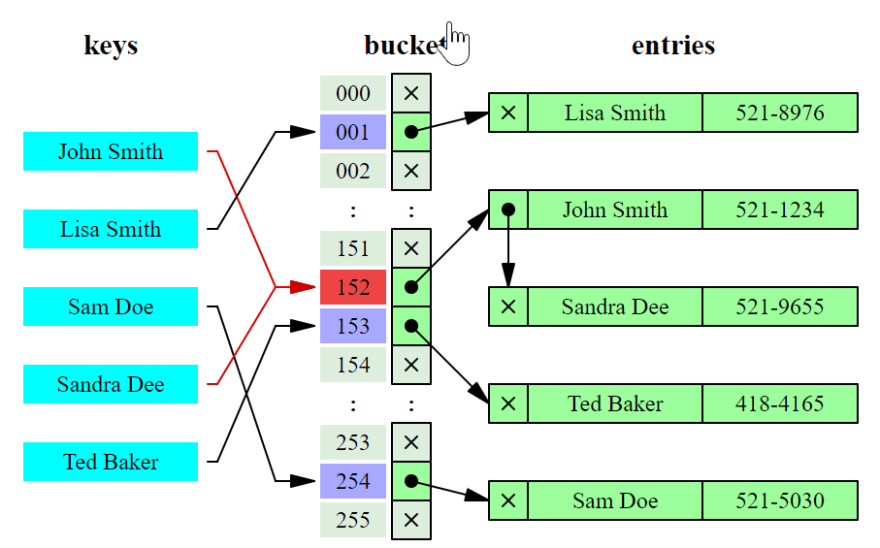
Ideally, the hash function will assign each key to a unique bucket, but most hash table designs employ an imperfect hash function, which might cause hash collisions where the hash function generates the same index for more than one key. Such collisions must be accommodated in some way.
Hash collision resolved by separate chaining.
Crucial Terms
- Key: A unique identifier for each value.
Value: The information we want to access (generally)
Note: You don't have to worry about the following terms to simply use a hash table, but you do need to know them to implement one (or to answer interview questions about how they're implemented!).Bucket: Depending on the implementation, this is either where the value data is stored, or a pointer to the value data is stored.
Sparseness: The property that the number of actual keys used is much smaller than the possible keys used. (e.g. there is an infinite number of strings that could be email addresses and only a finite number in use.)
Hash or hash-function: A function h(key) that takes the key and returns an index for the "bucket" containing the information that we want. The number of buckets is much smaller than the number of possible keys. Note this means that multiple keys are assigned to the same bucket. If there are K possible keys and B buckets, the average number of possible keys assigned to a given bucket is K/B.
Collision: When two keys k1 and k2 have the same hash (i.e. h(k1) == h(k2)) we say the keys collide, so they are assigned to the same bucket. There are different ways of storing different elements whose keys have the same hash.
Good hash: A good hash is a hash function that provides few collisions. Unfortunately, there is no universally good hash; the hash function has to be good for the distribution of keys that actually occur in your problem.
Strengths & Weaknesses
Hash tables combine random access ability with quick insertion and deletion, which makes it an extremely flexible and useful data structure. If you’re doing something other than storing keys and values, or if you need to sort elements or iterate efficiently through them, though, you should use a different data structure.
- Strengths
Note: These features assume the hashtable is sparse.
Hash tables have extremely fast lookup by key (O(1)).
Insertion and deletion of data is also quick (O(1)).
In a hash table, you can use the keys as the data, and use that to check if we've seen an element before. A hash table used this way is usually called a set.
- Weaknesses
Hash tables have no notion of order.
Hash tables cannot match "nearby" keys or keys that share the same prefix. So a hash table wouldn't be a good choice for checking for words that began with a certain prefix (a trie would be a better choice in that case).
Lookup by value (instead of by key) is O(n).
A hash table loses its strengths when the amount of data in a single bucket becomes large. Lookup becomes O(B), where B is the number of things in the bucket.
In Interviews, Use Hash Tables When...
There is a unique identifier that you use for lookup.
Examples:
Caller ID: Phone numbers are unique and can be used as a key to quickly retrieve a person. Note that we would not use a hash table that found a phone number given a person's name, since many people have the same name.
Car owner information: Using the license plate as a key, you can look up the owner of the car (the value).
You need to quickly determine if an element belongs to a collection. In these cases, you can represent the collection as a hash table with the elements as keys.
Example:
A Scrabble checker: If we want to determine if word is allowed, we could create a hash table valid_words where the keys were the words. We would set valid_words[w] = 1 for all valid words, so checking if word in valid_words is an O(1) operation.
You're dealing with problems about invariants.
Example:
To see if a word has an anagram, we can sort the letters of the string, and use it as a key in a hash table. (This method yields the same key for any two words that are anagrams of one another). The value can be a dummy value (if you're interested in the "yes/no" question of whether a word has an anagram) or an array of strings with the same key (if you are looking for the actual words).
Operation/ Descritpion /Time complexity /Mutates strutures
hash[key] = value : Add a new (key,value) pair to has table: O(1) : Yes
del hash[key] : Remove (key, value) from hash table: O(1) : Yes
key in hash: Lookup whenther key is in has table: O(1) : Yes
Note: Lookup by value is not supported directly in a hash table. Instead, you'd iterate through all the keys and check for the value you were looking for (an O(n) procedure).
References:
Hash Table
Hash Tables


Top comments (0)