JavaScript's Recursion Handling is Weird 🤷‍♂️

Recursion is one these things that you just have to accept before you understand it. However, once it clicked, it becomes an elegant way to solve problems, or to rephrase algorithms.

Memory-wise, recursion can be tricky. When used without care, recursion usually ends up causing stack overflow errors, as each call is added to the memory stack up on top of its ancestor - until the stack is out of space.

In order to prevent this scenario, it's preferable to use tail recursion.
This pattern dictates making the recursive call only at the very end of the recursive function. This allows the compiler (or engine, in the case of JavaScript) to optimize the function, so every recursive call frees its stack space once the next call is made.

Where Things Become Non-intuitive

When exemplifying recursion, the first thing that comes to mind is calculating the Fibonacci numbers.
Consider these two functions:

function fib1(n) {
  if (n === 1) return 0;
  if (n === 2) return 1;
  return fib1(n - 1) + fib1(n - 2);
};

function fib2(n) {
  return (() => {
    if (n === 1) return 0;
    if (n === 2) return 1;
    return fib2(n - 1) + fib2(n - 2);
  })();
};

Obviously they have the same output, although with a slight difference: fib2 contains a call an anonymous function that just wraps the same content of fib1.
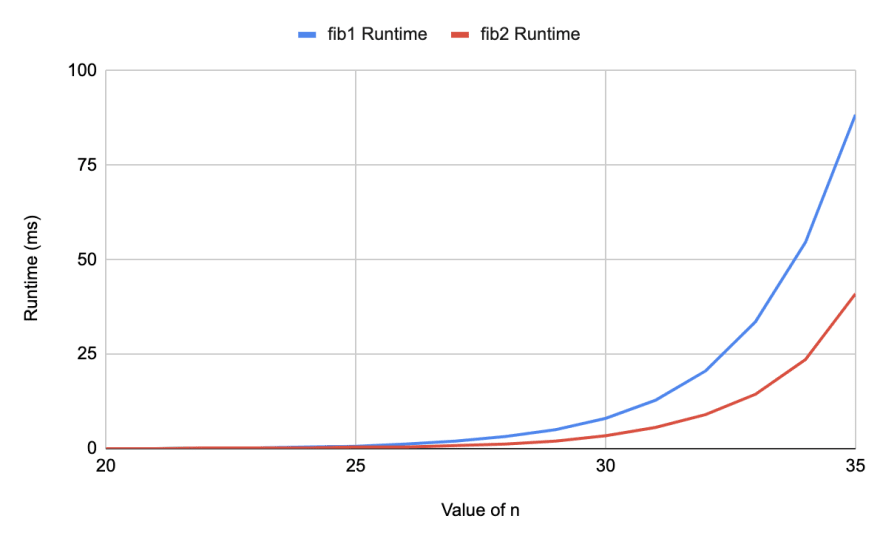
Apparently this minor change causes significant performance discrepancy: for lower n values the two function perform pretty much the same. Yet, around n = 25, the trend changes, so that fib2 becomes exponentially faster:

With tail recursion optimization in mind, it all makes sense. However, according to this table no JavaScript engine supports it (this conclusion is also backed by this StackOverflow answer).

And so we're left with one of JavaScript's unsolved mysteries. Every now and then, when this comes across my mind, it strikes me how even the world's most popular language has its weird issues that are deep under the hood, but potentially affects countless developers and applications.