Dijkstra's algorithm is used to find the shortest path(s) from node x to all its connected nodes.
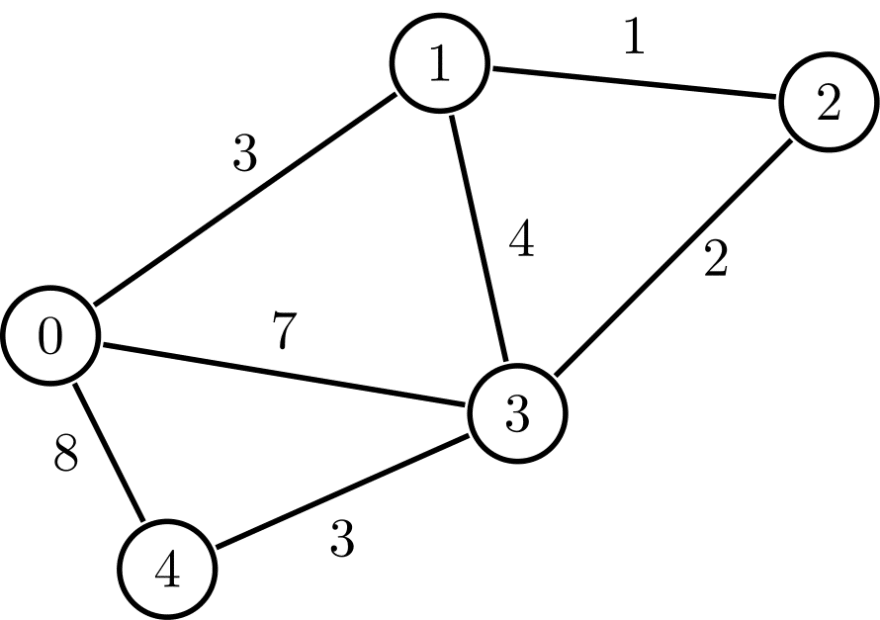
Consider the following weighted graph.
Whats the shortest path from node 0 to node 3?
We can look at the followings possible paths
7: 0 <--> 3
11: 0 <--> 4 <--> 3
7: 0 <--> 1 <--> 3
6: 0 <--> 1 <--> 2 <--> 3
The fourth path is the shortest path since we can look at the edges and see how long it will take to get there. But this is a small example, we can have graphs with millions of nodes and edges.
So how do we do this programmatically?
There are many algorithms for finding the shortest path between nodes within a graph but the focus here is Dijkstra's algorithm.
Implementation steps:
- Use DFS to visit the smallest nodes first.
- Compare parent distance and edge weight with node distance. In case it's less than infinity or calculated distance then update it.
- Use recursive programming to visit the smallest nodes.
Code:
Add Vertex and Path classes
data class Vertex(val name: String, var distance: Int = Int.MAX_VALUE, var visited: Boolean = false)
{
val linkedEdges = mutableListOf<Path>()
fun addEdges(edges: List<Path>) {
edges.sortedBy { it.weight }.forEach {
linkedEdges.add(it)
}
}
}
data class Path(val start: Vertex, val end: Vertex, val weight: Int)
Add a row class, this is used to print a table row at the end
data class DistanceRow(val to: String, val distance: Int, val via: String, ) {
override fun toString(): String {
return """
$to | $distance | $via
""".trimIndent()
}
}
Dijkstra's algorithm
class Dijkstra {
val distances = mutableListOf<DistanceRow>()
fun shortestPath(vertex: Vertex, d: Int = 0) {
vertex.visited = true
for (edge in vertex.linkedEdges) {
val distance = d + edge.weight
val connectedEdge = edge.end
if (distance < connectedEdge.distance) {
connectedEdge.distance = distance
distances.add(DistanceRow(connectedEdge.name, distance, vertex.name))
}
if (!connectedEdge.visited) {
shortestPath(connectedEdge, connectedEdge.distance)
}
}
}
}
Running the code
fun main() {
val zero = Vertex("0")
val one = Vertex("1")
val two = Vertex("2")
val three = Vertex("3")
val four = Vertex("4")
zero.addEdges(listOf(
Path(zero, one, 3),
Path(zero, four, 8),
Path(zero, three, 7),
))
one.addEdges(listOf(
Path(one, two, 1),
Path(one, three, 4),
))
two.addEdges(listOf(
Path(two, three, 2),
))
three.addEdges(listOf(
Path(three, two, 2),
))
four.addEdges(listOf(
Path(four, three, 3)
))
Dijkstra().apply {
shortestPath(zero)
print("Distances:\n---------------\nTo|Dist|Via\n---------------\n")
distances.forEach {
println(it)
}
}
}
Output:
Distances:
---------------
To|Dist|Via
---------------
1 | 3 | 0
2 | 4 | 1
3 | 6 | 2
4 | 8 | 0
Note: The example focuses on finding the shortest path from node 0 to node 3 therefore the edges have more connectivity between these nodes. Some edges are still undirected. Add directed edges for other nodes if needed.


Top comments (0)