Recursion is the method of a function calling itself, usually with a smaller dataset. Recursion is important because it often allows a breathtakingly simple algorithmic solution to certain problems that would otherwise be practically unobtainable with an iterative algorithm. Come along to check 11 Most Common Recursion Interview Questions with solutions for your next coding interview.
Originally published on FullStack.Cafe - Kill Your Next Tech Interview
Q1: Can you convert this Recursion function into a loop? ☆☆
Topics: Recursion
Problem:
Can you convert this recursion function into a loop?
A(x) {
if x<0 return 0;
return something(x) + A(x-1)
}
Solution:
Any recursive function can be made to iterate (into a loop) but you need to use a stack yourself to keep the state.
A(x) {
temp = 0;
for i in 0..x {
temp = temp + something(i);
}
return temp;
}
🔗 Source: stackoverflow.com
Q2: How Dynamic Programming is different from Recursion and Memoization? ☆☆
Topics: Dynamic Programming Recursion
Answer:
- Memoization is when you store previous results of a function call (a real function always returns the same thing, given the same inputs). It doesn't make a difference for algorithmic complexity before the results are stored.
- Recursion is the method of a function calling itself, usually with a smaller dataset. Since most recursive functions can be converted to similar iterative functions, this doesn't make a difference for algorithmic complexity either.
-
Dynamic programming is the process of solving easier-to-solve sub-problems and building up the answer from that. Most DP algorithms will be in the running times between a Greedy algorithm (if one exists) and an exponential (enumerate all possibilities and find the best one) algorithm.
- DP algorithms could be implemented with recursion, but they don't have to be.
- DP algorithms can't be sped up by memoization, since each sub-problem is only ever solved (or the "solve" function called) once.
🔗 Source: stackoverflow.com
Q3: Return the N-th value of the Fibonacci sequence Recursively ☆☆
Topics: Fibonacci Series
Answer:
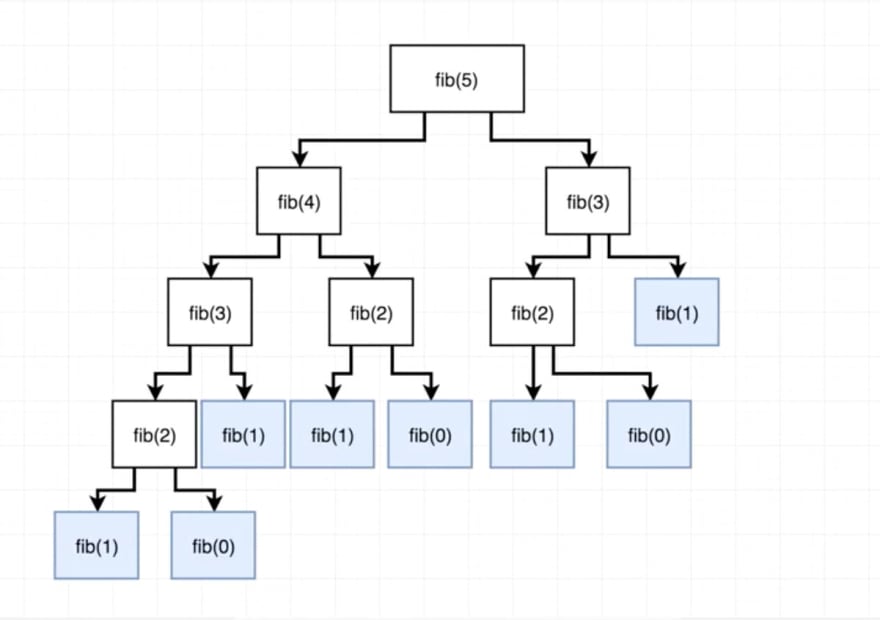
Recursive solution looks pretty simple (see code).
Let’s look at the diagram that will help you understand what’s going on here with the rest of our code. Function fib is called with argument 5:
Basically our fib function will continue to recursively call itself creating more and more branches of the tree until it hits the base case, from which it will start summing up each branch’s return values bottom up, until it finally sums them all up and returns an integer equal to 5.
Complexity Analysis:
Time Complexity: O(2^n)
In case of recursion the solution take exponential time, that can be explained by the fact that the size of the tree exponentially grows when n increases. So for every additional element in the Fibonacci sequence we get an increase in function calls. Big O in this case is equal to O(2n). Exponential Time complexity denotes an algorithm whose growth doubles with each addition to the input data set.
Implementation:
JS
function fib(n) {
if (n < 2){
return n
}
return fib(n - 1) + fib (n - 2)
}
Java
public int fibonacci(int n) {
if (n < 2) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}
PY
def F(n):
if n == 0: return 0
elif n == 1: return 1
else: return F(n-1)+F(n-2)
🔗 Source: medium.com
Q4: What is a good example of Recursion (other than generating a Fibonacci sequence)? ☆☆
Topics: Recursion
Answer:
There are some:
- The binary tree search
- Check for a palyndrome
- Finding factorial
- Traversing the folder hierarchy of a directory tree as part of a file system
- Towers of Hanoi
- Merge sort
- Catalan numbers
🔗 Source: stackoverflow.com
Q5: What is the difference between Backtracking and Recursion? ☆☆
Topics: Backtracking Recursion
Answer:
- Recursion describes the calling of the same function that you are in. The typical example of a recursive function is the factorial. You always need a condition that makes recursion stop (base case).
- Backtracking is when the algorithm makes an opportunistic decision, which may come up to be wrong. If the decision was wrong then the backtracking algorithm restores the state before the decision. It builds candidates for the solution and abandons those which cannot fulfill the conditions. A typical example for a task to solve would be the Eight Queens Puzzle. Backtracking is also commonly used within Neuronal Networks. Many times backtracking is not implemented recursively. If backtracking uses recursion its called **Recursive Backtracking*
P.S. Opportunistic decision making refers to a process where a person or group assesses alternative actions made possible by the favorable convergence of immediate circumstances recognized without reference to any general plan.
🔗 Source: www.quora.com
Q6: Convert a Binary Tree to a Doubly Linked List ☆☆☆
Topics: Binary Tree Linked Lists Recursion Divide & Conquer
Answer:
This can be achieved by traversing the tree in the in-order manner that is, left the child -> root ->right node.
In an in-order traversal, first the left sub-tree is traversed, then the root is visited, and finally the right sub-tree is traversed.
One simple way of solving this problem is to start with an empty doubly linked list. While doing the in-order traversal of the binary tree, keep inserting each element output into the doubly linked list. But, if we look at the question carefully, the interviewer wants us to convert the binary tree to a doubly linked list in-place i.e. we should not create new nodes for the doubly linked list.
This problem can be solved recursively using a divide and conquer approach. Below is the algorithm specified.
- Start with the root node and solve left and right sub-trees recursively
- At each step, once left and right sub-trees have been processed:
- fuse output of left subtree with root to make the intermediate result
- fuse intermediate result (built in the previous step) with output from the right sub-tree to make the final result of the current recursive call
Complexity Analysis:
Time Complexity: O(n)
Space Complexity: O(n)
Recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary tree h. It will be O(log n) for balanced tree and in worst case can be O(n).
Implementation:
Java
public static void BinaryTreeToDLL(Node root) {
if (root == null)
return;
BinaryTreeToDLL(root.left);
if (prev == null) { // first node in list
head = root;
} else {
prev.right = root;
root.left = prev;
}
prev = root;
BinaryTreeToDLL(root.right);
if (prev.right == null) { // last node in list
head.left = prev;
prev.right = head;
}
}
PY
def BinaryTreeToDLL(self, node):
#Checks whether node is None
if(node == None):
return;
#Convert left subtree to doubly linked list
self.BinaryTreeToDLL(node.left);
#If list is empty, add node as head of the list
if(self.head == None):
#Both head and tail will point to node
self.head = self.tail = node;
#Otherwise, add node to the end of the list
else:
#node will be added after tail such that tail's right will point to node
self.tail.right = node;
#node's left will point to tail
node.left = self.tail;
#node will become new tail
self.tail = node;
#Convert right subtree to doubly linked list
self.BinaryTreeToDLL(node.right);
🔗 Source: www.educative.io
Q7: Explain what is DFS (Depth First Search) algorithm for a Graph and how does it work? ☆☆☆
Topics: Backtracking Graph Theory Recursion
Answer:
Depth First Traversal or Depth First Search is a edge based recursive algorithm for traversing (visiting) all the vertices of a graph or tree data structure using a stack. The purpose of the algorithm is to mark each vertex as visited while avoiding cycles. DFS traverse/visit each vertex exactly once and each edge is inspected exactly twice. DFS is a genuinely recursive algorithm that uses stack for backtracking purposes, not for storing the vertex discovery "front" (as is the case in BFS).
The DFS algorithm works as follows:
- Start by putting any one of the graph's vertices on top of a stack.
- Take the top item of the stack and add it to the visited list.
- Create a list of that vertex's adjacent nodes. Add the ones which aren't in the visited list to the top of the stack.
- Keep repeating steps 2 and 3 until the stack is empty.
DFS example step-by-step:
- Considering A as the starting vertex which is explored and stored in the stack.
- B successor vertex of A is stored in the stack.
- Vertex B have two successors E and F, among them alphabetically E is explored first and stored in the stack.
- The successor of vertex E, i.e., G is stored in the stack.
- Vertex G have two connected vertices, and both are already visited, so G is popped out from the stack.
- Similarly, E s also removed.
- Now, vertex B is at the top of the stack, its another node(vertex) F is explored and stored in the stack.
- Vertex F has two successor C and D, between them C is traversed first and stored in the stack.
- Vertex C only have one predecessor which is already visited, so it is removed from the stack.
- Now vertex D connected to F is visited and stored in the stack.
- As vertex D doesn’t have any unvisited nodes, therefore D is removed.
- Similarly, F, B and A are also popped.
- The generated output is – A, B, E, G, F, C, D.
🔗 Source: techdifferences.com
Q8: Binet's formula: How to calculate Fibonacci numbers without Recursion or Iteration? ☆☆☆☆
Topics: Fibonacci Series
Answer:
There is actually a simple mathematical formula called Binet's formula for computing the nth Fibonacci number, which does not require the calculation of the preceding numbers:
It features the Golden Ratio (φ):
φ = (1+sqrt(5))/2
or
The iterative approach scales linearly, while the formula approach is basically constant time.
Complexity Analysis:
Time Complexity: O(log n)
Space Complexity: O(log n)
Assuming that the primitive mathematical operations (+, -, * and /) are O(1) you can use this result to compute the nth Fibonacci number in O(log n) time (O(log n) because of the exponentiation in the formula).
Implementation:
CS
static double inverseSqrt5 = 1 / Math.Sqrt(5);
static double phi = (1 + Math.Sqrt(5)) / 2;
/* should use
const double inverseSqrt5 = 0.44721359549995793928183473374626
const double phi = 1.6180339887498948482045868343656
*/
static int Fibonacci(int n) {
return (int)Math.Floor(Math.Pow(phi, n) * inverseSqrt5 + 0.5);
}
JS
const sqrt = Math.sqrt;
const pow = Math.pow;
const fibCalc = n => Math.round(
(1 / sqrt(5)) *
(
pow(((1 + sqrt(5)) / 2), n) -
pow(((1 - sqrt(5)) / 2), n)
)
);
Java
private static long fibonacci(int n) {
double pha = pow(1 + sqrt(5), n);
double phb = pow(1 - sqrt(5), n);
double div = pow(2, n) * sqrt(5);
return (long)((pha - phb) / div);
}
PY
def fib_formula(n):
golden_ratio = (1 + math.sqrt(5)) / 2
val = (golden_ratio**n - (1 - golden_ratio)**n) / math.sqrt(5)
return int(round(val))
🔗 Source: pi3.sites.sheffield.ac.uk
Q9: Calculate n-th Fibonacci number using Tail Recursion ☆☆☆☆
Topics: Fibonacci Series
Answer:
In traditional recursion, you perform the recursive call, take the return value of that call and calculate the results. You get the results of your calculation only until you’ve returned from every recursive call, requiring a lot of space on the call stack:
function fib(n){
if (n === 1) return 0;
if (n === 2) return 1;
return fib(n — 1) + fib(n — 2);
}
In tail recursion, you calculate the results first, and pass the results of your current call onto the next recursive call:
function fib(n, a = 0, b = 1){
if (n > 0) {
return fib(n - 1, b, a + b)
}
return a
}
Now, when you are ready to calculate the next call, you don’t need the current stack frame. You are calculating the results and passing them as parameters to your next call. No more worries about stack overflow!
This tail recursive solution is constant O(n) time and constant O(n) space complexity.
Implementation:
JS
function fib(n, a = 0, b = 1){
if (n > 0) {
return fib(n - 1, b, a + b)
}
return a
}
Java
private static final int FIB_0 = 0;
private static final int FIB_1 = 1;
private int calcFibonacci(final int target) {
if (target == 0) { return FIB_0; }
if (target == 1) { return FIB_1; }
return calcFibonacci(target, 1, FIB_1, FIB_0);
}
private int calcFibonacci(final int target, final int previous, final int fibPrevious, final int fibPreviousMinusOne) {
final int current = previous + 1;
final int fibCurrent = fibPrevious + fibPreviousMinusOne;
// If you want, print here / memoize for future calls
if (target == current) { return fibCurrent; }
return calcFibonacci(target, current, fibCurrent, fibPrevious);
}
🔗 Source: medium.com
Q10: How to recursively reverse a Linked List? ☆☆☆☆
Topics: Linked Lists Recursion
Answer:
Start from the bottom up by asking and answering tiny questions:
- What is the reverse of
null(the empty list)?null. - What is the reverse of a one element list? the element.
- What is the reverse of an n element list? the reverse of the rest of the list followed by the first element.
P.S.
How to understand that part?
head.next.next = head;
head.next = null;
Think about the origin link list:
1->2->3->4->5
Now assume that the last node has been reversed. Just like this:
1->2->3->4<-5
And this time you are at the node 3 , you want to change 3->4 to 3<-4 , means let 3->next->next = 3 (as 3->next is 4 and 4->next = 3 is to reverse it)
Complexity Analysis:
Time Complexity: O(n)
Space Complexity: O(n)
Assume that n is the list's length, the time complexity is O(n). The extra space comes from implicit stack space due to recursion. The recursion could go up to n levels deep then space complexity is O(n).
Implementation:
JS
var reverseList = function(head) {
if (!head) {
return head;
}
let pre = head.next;
head.next = null;
return fun(head, pre);
function fun(cur, pre) {
if (pre == null) {
return cur;
}
let tmp = pre.next;
pre.next = cur;
return fun(pre, tmp);
}
}
Java
Node reverse(Node head) {
// if head is null or only one node, it's reverse of itself.
if ( (head == null) || (head.next == null) ) return head;
// reverse the sub-list leaving the head node.
Node reverse = reverse(head.next);
// head.next still points to the last element of reversed sub-list.
// so move the head to end.
head.next.next = head;
// point last node to nil, (get rid of cycles)
head.next = null;
return reverse;
}
PY
class Solution(object):
def reverseList(self, head): # Recursive
"""
:type head: ListNode
:rtype: ListNode
"""
if not head or not head.next:
return head
p = self.reverseList(head.next)
head.next.next = head
head.next = None
return p
🔗 Source: stackoverflow.com
Q11: How to use Memoization for N-th Fibonacci number? ☆☆☆☆
Topics: Dynamic Programming Fibonacci Series Recursion
Problem:
Why? Any problems you may face with that solution?
Solution:
Yes. It's called Memoization. Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls.
Let’s look at the diagram that will help you understand what’s going on here with the rest of our code. Function fib is called with argument 5. Can you see that we calculate the fib(2) results 3(!) times?
Basically, if we just store the value of each index in a hash, we will avoid the computational time of that value for the next N times. This change will increase the space complexity of our new algorithm to O(n) but will dramatically decrease the time complexity to 2N which will resolve to linear time since 2 is a constant O(n).
There’s just one problem: With an infinite series, the memo array will have unbounded growth. Eventually, you’re going to run into heap size limits, and that will crash the JS engine. No worries though. With Fibonacci, you’ll run into the maximum exact JavaScript integer size first, which is 9007199254740991. That’s over 9 quadrillion, which is a big number, but Fibonacci isn’t impressed. Fibonacci grows fast. You’ll burst that barrier after generating only 79 numbers.
Complexity Analysis:
Time Complexity: O(n)
Space Complexity: O(n)
Implementation:
JS
function fibonacci(num, memo) {
memo = memo || {};
if (memo[num]) return memo[num];
if (num <= 1) return 1;
return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);
}
Java
static int fibMemo[];
public static int fibByRecMemo(int num) {
if (num == 0) {
fibMemo[0] = 0;
return 0;
}
if (num == 1 || num == 2) {
fibMemo[num] = 1;
return 1;
}
if (fibMemo[num] == 0) {
fibMemo[num] = fibByRecMemo(num - 1) + fibByRecMemo(num - 2);
return fibMemo[num];
} else {
return fibMemo[num];
}
}
🔗 Source: medium.com
Q12: Is it always possible to write a non-recursive form for every Recursive function? ☆☆☆☆
Topics: Recursion
Answer:
When you use a function recursively, the compiler takes care of stack management for you, which is what makes recursion possible. Anything you can do recursively, you can do by managing a stack yourself (for indirect recursion, you just have to make sure your different functions share that stack).
A simple formal proof is to show that both µ recursion (general recursive function) and a non-recursive calculus such as GOTO are both Turing complete. Since all Turing complete calculi are strictly equivalent in their expressive power, all recursive functions can be implemented by the non-recursive Turing-complete calculus.
🔗 Source: stackoverflow.com
Thanks 🙌 for reading and good luck on your interview! Please share this article with your fellow Devs if you like it! Check more FullStack Interview Questions & Answers on 👉 www.fullstack.cafe





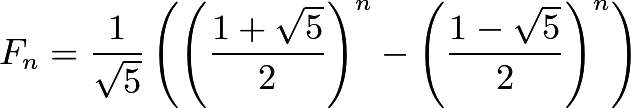


Top comments (0)