Binary Search Tree - Insert, Lookup and Remove

Binary search trees (BSTs) are a sort of data structure that is used to store and search for data effectively. A BST is a tree structure with no more than two children: a left child and a right child. The left child is always smaller than the parent node, whereas the right child is always greater than the parent node. The most significant feature of a BST is that it enables efficient searching. This is due to the BST's recursive nature, which enables binary search methods to be implemented. We shall look at the explanation of a BST and its insert, lookup and remove methods in Python

Basic Concepts

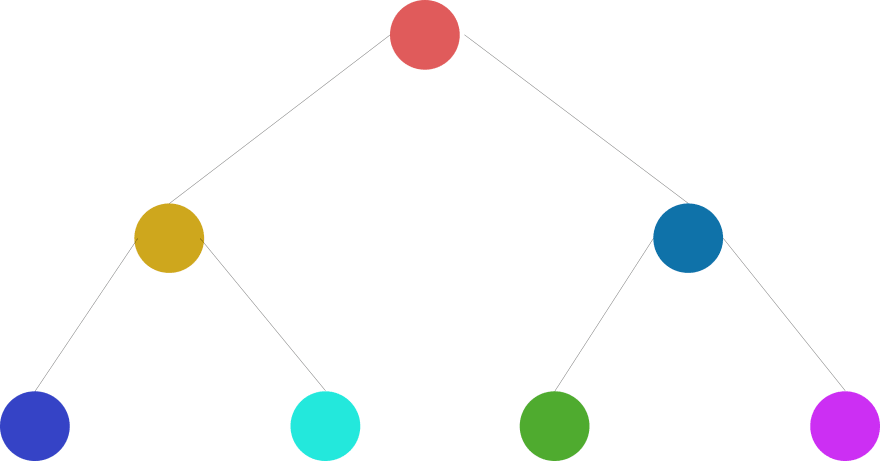
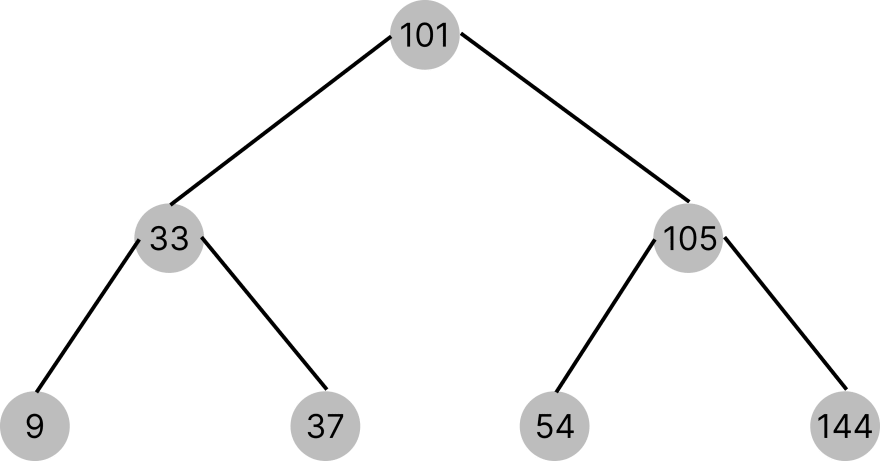
Binary Search Trees are made up of nodes and edges. The nodes are the various points in the memory that holds the data. In the diagram below, the colored circles are the nodes and the black lines connecting them are the edges.

Root Nodes

The root node of a BST is the first node. It is called root because all other nodes in the BST originate from this root node. In the example above, node 101 is the root node.

Leaf Nodes

In a BST, the leaf nodes are nodes that do not have either a left child or a right child. They are the last node in the tree and they are of great importance in a BST. From the example above, nodes 9, 37, 54 and node 144 are leaf nodes.

Parent Nodes

Parent nodes in a BST are nodes that have either a left child or right child or even both children. In the example above, node 33 is the parent node of nodes 9 and 7, and node 105 is the parent node of nodes 54 and 144. The root node is also a parent node and it is the parent node of nodes 33 and 105.

BST Methods

In a BST, there are three main methods which are insert, lookup and remove. These methods are used to insert, find and remove a node respectively. We will now look at how to implement these methods.

Node Class

Since a BST is made up of different nodes, we need to first define our node class

class Node:
    def __init__(self, value):
        self.left = None
        self.right = None
        self.value = value

    def __repr__(self):
        return str(self.__dict__)

In this code snippet above, the node has a left and right pointer as well as the value it will hold. It also has a 'repr' class that we are implementing to determine how we want to output our node. In this case, we are choosing it to be a python dictionary or an object.

Binary Search Tree Class

class BinarySearchTree():
    def __init__(self) -> None:
        self.root = None

    def __repr__(self) -> None:
        return str(self.__dict__)

Here we are just stating the constructor for the BST class and also implementing our choice of output. By default, the BST object we are creating is going to have a root node.

Insert Method

def insert(self, value):
        newNode = Node(value)
        if self.root == None:
            self.root = newNode
            return
        currentNode = self.root
        while True:
            if currentNode.value > newNode.value:
                if currentNode.left == None:
                    currentNode.left = newNode
                    return
                currentNode = currentNode.left
            if currentNode.value < newNode.value:
                if currentNode.right == None:
                    currentNode.right = newNode
                    return
                currentNode = currentNode.right

We first check if the tree is empty by evaluating the value of the root property. Since we do not know where we are going to end, if the currentnode's value is greater than the newnode's value, we also check if there is an already existing direct child node to the left of the currentnode. If there is no node, we insert the newnode there or we continue to traverse to the leftmost node of the currentnode. We also do the same thing for the right subtree of the node by checking if the currentnode's value is less than the newnode's value. Then we perform the same operation but this time, we will be traversing to the rightmost node.

Lookup Method

def lookup(self, value):
        if self.root == None:
            print("Empty Tree")
            return
        currentNode = self.root
        while currentNode:
            if currentNode.value > value:
                currentNode = currentNode.left
            elif currentNode.value < value:
                currentNode = currentNode.right
            elif currentNode.value == value:
                print("Found")
                return currentNode
        print("Not Found")
        return None

In this lookup method, we check if the tree is empty, else we continue to look for the node by comparing the value of the currentnode to the value we are looking for. If the currentnode is greater than the value we are looking for, then we going leftward and if the currentnode is smaller than the value, then we are going right.

Remove method

This is the trickiest and longest method, but we are going to discuss it together. When you want to delete a node from a BST. YOu would be faced with any of the following three scenarios:

• If the node has no children - Just delete it.
• If the node has a single child - Copy that child to the node.
• If the node has two children - Determine the next highest element in the right subtree. Replace the node to be removed with the next highest node. Delete the next node. So we find the leftmost node of the right subtree of the current node. This leftmost node can be found by looping from the current node to the last node (until when there is no left node). This will reduce the problem to a scenario where the node has only one child or no child.

    def remove(self, value):
        if self.root == None:
            return "Empty List"
        currentNode = self.root
        parentNode = None
        while currentNode != None:
            if currentNode.value > value:
                parentNode = currentNode
                currentNode = currentNode.left
            elif currentNode.value < value:
                parentNode = currentNode
                currentNode = currentNode.right
            else: # A match has been found
                # Both left and right children
                if currentNode.left != None and currentNode.right != None:
                    badNode = currentNode.right
                    badNodeParent = currentNode.right
                    while badNode.left != None:
                        badNodeParent = badNode
                        badNode = badNode.left
                    currentNode.value = badNode.value
                    if badNode == badNodeParent:
                        currentNode.right = badNode.right
                    if badNode.right == None:
                        badNodeParent.left = None
                        return
                    else:
                        badNodeParent.left = badNode.right
                        return

                # No left or right children
                elif currentNode.left == None and currentNode.right == None:
                    if parentNode == None:
                        self.root = None
                        return
                    if parentNode.value > currentNode.value:
                        parentNode.left = None
                        return
                    else:
                        parentNode.right = None
                        return

                # Only left child
                elif currentNode.left != None and currentNode.right == None:
                    if parentNode == None:
                        self.root = None
                        return
                    if parentNode.value > currentNode.value:
                        parentNode.left = currentNode.left
                        return
                    else:
                        parentNode.right = currentNode.left
                        return

                # Only right child
                elif currentNode.left == None and currentNode.right != None:
                    if parentNode == None:
                        self.root = None
                    if parentNode.value > currentNode.value:
                        parentNode.left = currentNode.right
                        return
                    else:
                        parentNode.right = currentNode.right
                        return

The Time Complexity of BST operations is O(h). h is the height of the tree.

The source code for this tutorial can be found at https://github.com/valentinesamuel/EssentialOrigin/blob/main/test_ds/binary_search_tree.py

Conclusion

It is crucial to note, however, that the effectiveness of a BST is dependent on the structure of the tree. The efficiency of operations can be dramatically lowered if the tree is imbalanced (i.e., one subtree is significantly bigger than the other). There are numerous approaches for balancing BSTs, such as AVL trees and red-black trees, to address this issue. These strategies will be detailed in a subsequent post.

Don't forget to leave a like or comment. Till next time guys.

❤️❤️❤️

Resume Portfolio Twitter GitHub LinkedIn