Rdv manqué entre Koh Lanta et les maths

Le Mardi 26 avril 2022, TF1 diffusait la seconde partie de son épisode des ambassadeurs de Koh Lanta. Cette saison est marquée par l'empreinte du totem maudit. À chaque épreuve de confort, l'équipe perdante se voit attribuer un gage. À l'occasion de la réunification, les règles du tirage au sort entre les ambassadeur.rice.s s'ils ne se mettaient pas d'accord sur un.e aventurier.e à éliminer, ont changé.

Rappel du contexte

Koh Lanta est une émission de téléréalité diffusée par TF1 depuis 20 ans. Une vingtaine de participant.e.s doivent survivre sur une île déserte, tout en éliminant un aventurier.e régulièrement. Le gagnant est alors élu par les derniers aventurier.e.s.
Au départ iels sont répartis dans 2 équipes (parfois 3 au début, mais on revient à 2 à un moment du jeu). Puis vient le moment de la réunification où les 2 équipes n'en forme plus qu'une. Mais... Un.e aventurier.e doit être désigné éliminé (et non pas élu). Pour se faire, un.e aventurier.e de chaque équipe, appelé ambassadeur.rice.s, se réunissent pour discuter et choisir la personne à faire sortir.
Chaque équipe doit défendre son bout de gras, car arriver en minorité à la réunification signifie moins de chances pour les membres de son équipe de rester dans la partie.
Aussi, si les ambassadeur.e.s ne peuvent se mettre d'accord, un tirage au sort est lancé entre eux deux.
Une boule blanche et une noire, celui qui tir la noire, chao.

La malédiction du totem

Cette année, les aventurier.ère.s désignés ont été : Louana pour les rouges, et Colin pour les jaunes.
Le totem maudit est venu altérer le tirage au sort pour handicaper l'équipe jaune, ayant perdu l'épreuve de confort d'avant.

2 sachets, un rouge et un jaune, sont présents. Dans le rouge, une boule blanche et une boule noire. Dans le jaune, maudit, une boule blanche et deux boules noires.
Le tirage au sort se déroule ainsi :
À l'aveugle, Louana tire une boule dans le sachet rouge et Colin tire une boule dans le sachet jaune.
Si les boules sont de la même couleur, alors on replace les boules dans leur sachet respectif, et on recommence le tirage.
Si les boules sont de couleur différente, alors celui ou celle qui tire la noire est éliminé.

Question : quel est le risque pour chacun.e des ambassadeur.rice.s d'être éliminé lors du tirage au sort ?

Lors de l'émission, Denis, le présentateur, affirme que Louana à 50% de risque d'être éliminée, contre 66% pour Colin.
Problème, la somme ne fait pas 100%, mais 116%.
Selon vous, s'est-il trompé ? Et si oui, quels sont les vrais risques ?

En vrai, la formulation de Denis est trompeuse, car il n'annonce pas le risque d'être éliminé, mais la probabilité de tirer une boule noire. Ce qui, nous allons le voir, est légèrement différent, et pas aussi simple qu'il n'y paraît.

Formalisation du problème

Pour la suite, nous noterons :

• L : l'évènement Louana est éliminée
• C : l'évènement Colin est éliminé
• R : l'évènement on Recommence le tirage
• $P(L)$ : la probabilité que Louana soit éliminée,
• $P(C)$ : la probabilité que Colin soit éliminé,
• $P(L_n)$ : la probabilité que Louana soit éliminée au bout de n tirages,
• $P(C_n)$ : la probabilité que Colin soit éliminé au bout de n tirages,
• $P(R_n L)$ : la probabilité que Louana soit éliminée sachant qu'on a recommencé le tirage n fois,
• $P(R_n C)$ : la probabilité que Colin soit éliminé sachant qu'on a recommencé le tirage n fois,
• $P(R_n R)$ : la probabilité que l'on recommence le tirage sachant qu'on a recommencé le tirage n fois.

Dénombrement du $1^{er}$ tirage

L'ensemble des évènements possibles lors du premier tirage peut être résumé par ce tableau :

o boule blanche tirée
• boule noire tirée

Sachant qu'on n'a pas encore recommencé de tirage, on a alors :

• $P(R_0L) = {^1/_6}$
• $P(R_0C) = {^1/_3}$
• $P(R_0R) = {^1/_2}$

On peut donc commencer à estimer les risques d'élimination de Louana et Colin :

• $P(L_0) = P(R_0L) = {^1/_6}$
• $P(C_0) = P(R_0C) = {^1/_3}$

Premier constat : au premier tirage, Colin a moins de risques d'être éliminé qu'avec un tirage classique.
Oui mais voilà, lorsque l'événement R se produit, on refait le tirage, dans les mêmes conditions. Et ce que nous dis la théorie des probabilités, c'est que les probabilités restent les mêmes pour ce second tirage.

Dénombrement du $2^{ème}$ tirage

Après le second tirage, on obtient les probabilités de ces évènements :

• $P(R_0L) = {\frac{1}{6}}$
• $P(R_0C) = {\frac{1}{3}}$
• $P(R_1L) = {\frac{1}{2}} \times {\frac{1}{6}} = {^1/_{12}}$
• $P(R_1C) = {\frac{1}{2}} \times {\frac{1}{3}} = {^1/_6}$
• $P(R_1R) = {\frac{1}{2}} \times {\frac{1}{2}} = {^1/_4}$

On peut donc ré-estimer les risques d'élimination de Louana et Colin après avoir recommencé 1 tirage :

• $P(L_1)=P(R_0L) + P(R_1L) = {^1/_4}$
• $P(C_1)=P(R_0C) + P(R_1C) = {^1/_2}$

Dénombrement du $n^{ème}$ tirage

On peut généraliser ces formules sur n tirage pour être encore plus précis :

• $P(L_n)=P(R_0L)+P(R_1L)+...+P(R_nL)=\frac{1}{6} \times (1+{\frac{1}{2}}+{\frac{1}{4}}+...+({\frac{1}{2}})^n)$
• $P(C_n)=P(R_0C)+P(R_1C)+...+P(R_nC)=\frac{1}{3} \times (1+{\frac{1}{2}}+{\frac{1}{4}}+...+({\frac{1}{2}})^n)$

ou écrit plus formellement :

• $P(L_n)=\sum_{i=0}^{n} P(R*iL)={\frac{1}{6}} \times \sum_{i=0}^{n} ({\frac{1}{2}})^i$
• $P(C_n)=\sum_{i=0}^{n} P(R*iC)={\frac{1}{3}} \times \sum_{i=0}^{n} ({\frac{1}{2}})^i$

Simplification des formules

On peut simplifier cette somme de puissance de $\frac{1}{2}$ en utilisant la somme des termes d'une suite géométrique de raison 1/2, et de premier terme 1 :

$\sum_{i=0}^{n} ({\frac{1}{2}})^i = \frac{1-({\frac{1}{2}})^{n+1}}{1-\frac{1}{2}}$

D'où :

• $P(L_n)=\frac{1}{3} \times (1-(\frac{1}{2})^{n+1})$
• $P(C_n)=\frac{2}{3} \times (1-(\frac{1}{2})^{n+1})$

Analyse des résultats

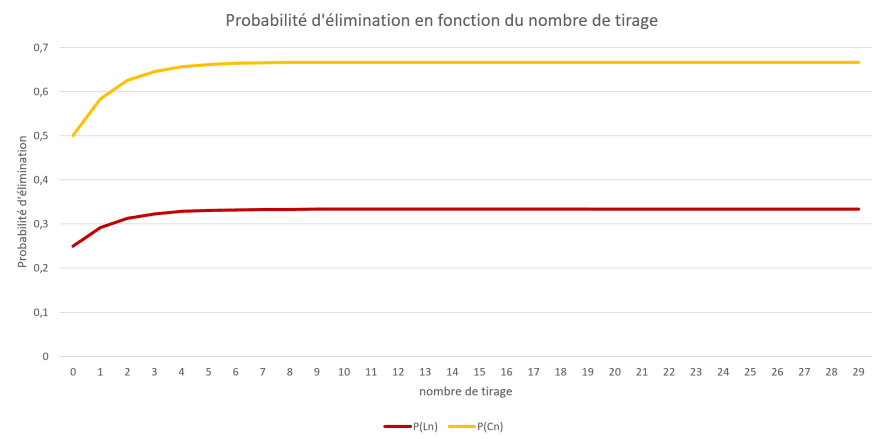
Si on trace les valeurs successives de ces probabilités, on obtient :

On constate que ces probabilités convergent, c'est-à-dire que plus n est grand, plus leur valeur se rapproche d'un nombre.

L'idéal serait alors de calculer ces probabilités pour un nombre infini de tirage. Ça tombe bien, il y a un concept pour ça en maths, c'est la limite.

Vers l'infini et au-delà

• $P(L)=\lim_{n\to + \infty} P(L_n)= \lim_{n\to + \infty} \frac{1}{3}\times (1-(\frac{1}{2})^{n+1})$
• $P(C)=\lim_{n\to + \infty} P(C_n)= \lim_{n\to + \infty} \frac{2}{3}\times (1-(\frac{1}{2})^{n+1})$

Or $\lim_{n\to + \infty} (\frac{1}{2})^{n+1} =0$

Donc

• $P(L)={^1/_3}$
• $P(C)={^2/_3}$

Conclusion

Au final, Louana avait 1 risque sur 3 d'être éliminée (ou ~33%), contre 2 sur 3 pour Colin (ou ~66%).

Dit autrement, Colin avait 2 fois plus de risque d'être éliminé que Louana dans ce tirage au sort.

D'un simple problème de tirage au sort, nous avons utilisé la somme des termes d'une suite géométrique et un calcul de limite.

Qui a dit que les maths ne servait à rien ? Même en regardant TF1 on peut en avoir besoin 😉.