This story contains the anecdote behind how I came across the quirkiness of JS number during the development of a personal finance app.
As the application would grow and populate more numeric data, I came to wonder how commercial finance applications deal with fraction points of currencies. This question was derived from the multiple fraction point numbers after all the money values tallied up by JavaScript. When building a commercial application, this would be a prime discussion among developers, accountants and other stakeholders. As result of my lack of time and expertise in finance, I wasn’t sure how to approach to this issue and couldn’t conduct significant research. Considering this is a premature version of a personal finance app which doesn’t set out any rules in terms of any complex financial covenants, I just decided to keep it simple for now. Furthermore, the current implementation wouldn’t have a great effect on the actual monetisation of the users’ financial flow in a direct manner.
Putting aside how to define the fraction numbers, the reason why the aggregated result from JavaScript returns the unexpected fraction numbers was investigated.
This would be an example of the quirkiness of JavaScript numbers. Wouldn't you expect the result would be 58.87 if you have learn the basic arithmetic from school unless you are a CS student or a well-versed developer?
As I understand it, all computational processes run with binary code and representational data such as images, audio, characters and numbers which are stored as binary and are encoded in different formats to deliver their means. Specifically, JavaScript encodes all the numeric values with double precision floating point numbers(64 bit) following IEEE Standard. Even though we may expect the aggregate result from the example above to simply be 58.87, it returns all the fraction points by the nature of how JavaScript processes numeric value with double-precision floating point number. As such I decided to delve into this further to provide rationale and to advocate my decision regarding rounding up/down fraction numbers.
Photo by Alexander Sinn on Unsplash
IEEE754 Double-Precision binary floating-point format : Binary64

[¹] Significand precision is implicitly 53 bits. However, 1 bit is not stored since it goes through the normalisation and it always leads with value “1”. It’s called implicit bit, hidden bit and so on.
JavaScript has adapted Double-Precision floating point format as its standard for numbers. As we can conjecture from its naming, this format provides a wider range of numbers and higher accuracy compared to single-precision or half-precision floating-point format.
Specifically speaking, JavaScripts can process numbers in the range between Number.MAX_SAFE_INTEGER(253 - 1) and Number.MIN_SAFE_INTEGER(-(253 - 1)) based on the binary 64 format. However, ECMAScript 2020 which was published in June 2020 updated their specification and it includes a new built-in object BigInt which provides a larger number representation for JavaScript.
Naturally this format takes up more memory and requires a better processor to perform this computation. During this research, I also learned how to convert binary to denary and vice versa. This was a very constructive learning in order to understand the quirkiness of JavaScript Number. As such I’d like to articulate how the denary number is converted to 64bit binary number under the hood.
Denary 19.25
First, Convert the whole number 19 to binary : divide the number until the remainder is 0/1.
The Converted binary is 10011.
Read the remainders from bottom to top for the whole number.
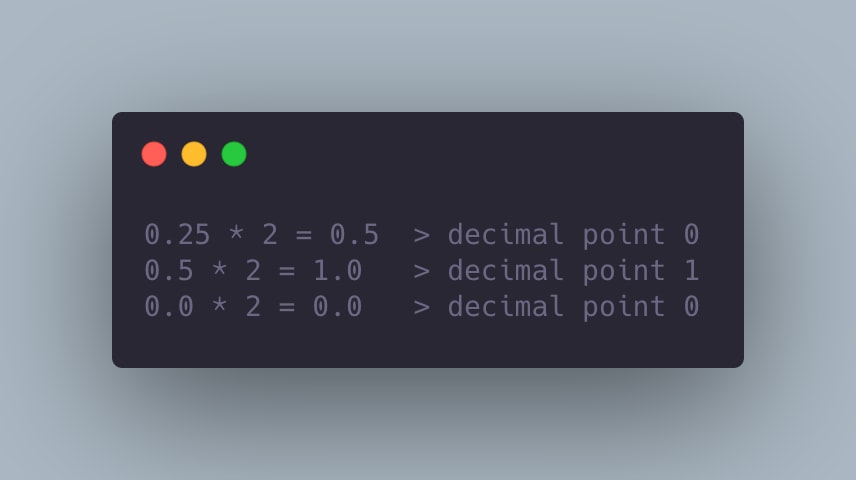
Secondly, Convert the fraction number 0.25 to binary : multiply the fraction numbers by 2 until the value returns to 0.
The Converted binary is 0.01.
Read the decimal points from top to bottom at this time
Thirdly, Combine the two parts of the number and Normalise for significand and unbiased exponent (move the binary point to after leftmost 1 or to the right where the first “1” value exists) : Once the binary numbers are normalised, the number of times we moved the decimal point to the leftmost 1[²]will be the exponent in the base 2 notation.
10011.01 = 1.001101 × 2⁴
[²] If whole number conversion to binary starts with a decimal point, for example, 0.00110011, you need to move the decimal point to the right where the first “1” value is located. In this case, the result will be 1.10011 × 2⁻³
Fourthly, Get the biased exponent based on precision.
4 + 1023 = 1027₁₀ = 10000000011 ₂
Read the remainders from bottom to top just like the first step we did.
Fifthly, Determine the significand removing leading 1 from step 3.
1.001101
Finally, we have successfully converted Decimal number 19.25 to Binary64 format.
Now, I will convert a 64bit binary to the denary value which is a simplified demonstration to show you how the computer processes this under the hood.
64bit binary
For an easier explanation, refer to this table.

e = 2¹⁰ + 2⁰ = 1024 + 1 = 1025₁₀
p = e - 1023 = 2
p indicates precision.
The first column indicates the implicit significand value 1 which is called implicit bit[¹] and the value we get from the biased exponent subtracting the unbiased exponent denotes where the bit index starts from. If the exponent values are positive, move towards the right-hand side and if negative, move towards the left-hand side from the implicit bit as you can see on the table. Now, we have the denary value, 5.
n = 2² + 2⁰ = 4 + 1 = 5
If the number value is just an integer like in the example above, the calculation is straightforward. However, decimal is more complicated and it sometimes requires rounding up/down depending on the last value of significand.
64bit binary
e = 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2⁰
= 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 1
= 1021₁₀
p = e - 1021 = -2
p indicates precision.
This time exponent value is negative. So, we need to move to the left hand side two times.

purple cells denotes its repetitions of the pattern.
n = 2⁻² + 2⁻⁵ + 2⁻⁶ + 2⁻⁹ + 2⁻¹⁰ + 2⁻¹³ + 2⁻¹⁴ + 2⁻¹⁷ + 2⁻¹⁸ + 2⁻²¹ 2⁻²² + 2⁻²⁵ + 2⁻²⁶ + 2⁻²⁹ + 2⁻³⁰ + 2⁻³³ + 2⁻³⁴ + 2⁻³⁷ + 2⁻³⁸ + 2⁻⁴¹ + 2⁻⁴² + 2⁻⁴⁵ + 2⁻⁴⁶ + 2⁻⁴⁹ + 2⁻⁵⁰ + 2⁻⁵³ + 2⁻⁵⁴
= - 0.3
By the nature of binary and the larger bit binary deals with a wider range of fraction values for higher accuracy and precision, tallying-up the value of fraction point numbers by JavaScript returns quirky(?) values unlike we would expect.

















Top comments (0)