Solving problems with Binary Search algorithm
Binary search algorithm is widely used. It can be very simple but you can be confused with some implementation details.
If you check the Leetcode website you will see that binary search is used to help solve more than 150 problems (https://leetcode.com/tag/binary-search). In this article we are going to see how to implement the algorithm and after that we are going to find the solution to an easy problem from the Leetcode that can be solved using the binary search. Easy level problems are usually not so complex as medium or hard, so we can concentrate on the algorithm itself rather than details of the solution.
Implementation
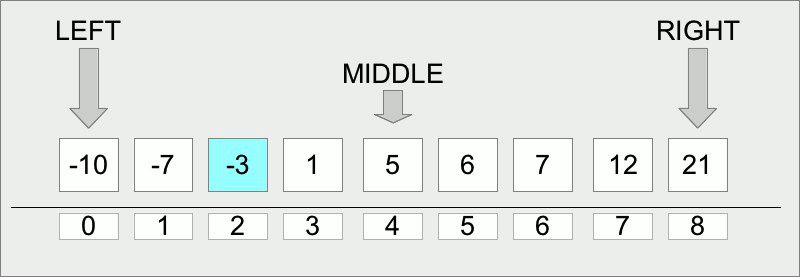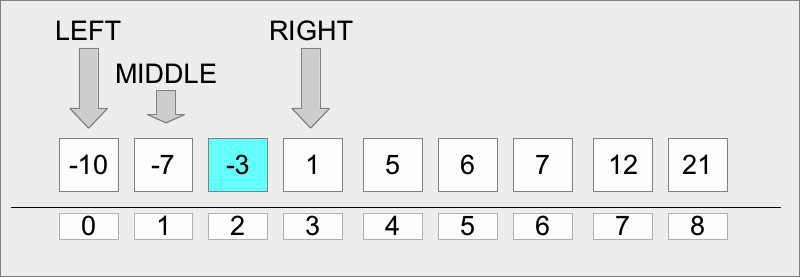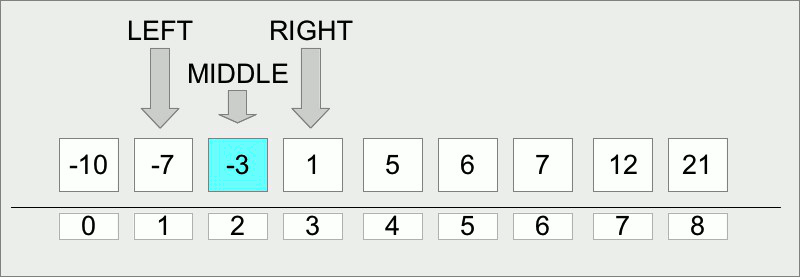
Let us start with the implementation of the algorithm. Binary search is intended to find a target value (its position) within an array (which should be sorted, usually in ascending order). The main idea of the algorithm is to check if the value in the middle of the array is equal to the target. If so we have found the target value and its index. If the current middle element value is more than the target value then we need to check the middle element in the left part of the current slice of the array, in other case we need to check it in the right part. On each step the slice size decreases by two times. The algorithm stops when the target value is found or when the slice size cannot be decreased. In the last case the element is not found in the array.
Binary search algorithm has O(logN) (because we decrease search area by two times on each iteration) time complexity and O(1) memory complexity (as we need only three pointers to implement it) keeping in mind that we need the sorted array as an input. So if our input is unsorted it will usually take O(NlogN) time to sort the input array.
Now it is time to implement the binary search. The usual implementation looks like this:
LEFT = 0
RIGHT = LENGTH(ARRAY)-1
WHILE LEFT <= RIGHT DO
MIDDLE = (LEFT + RIGHT) / 2
IF ARRAY[MIDDLE] > TARGET THEN
RIGHT = MIDDLE - 1 // element on the left side
ELSE IF ARRAY[MIDDLE] < TARGET THEN
LEFT = MIDDLE + 1 // element on the right side
ELSE
RETURN MIDDLE // element found
END IF
END WHILE
RETURN -1 // element not found
We can find golang code here: https://github.com/emikhalev/algorithm/tree/master/algorithms/binary_search (binary_search.go). We need to pay attention to the test as it contains most pitfalls and corner cases (binary_search_test.go).
Problem Solving
Let us now solve the “Find Target Indices After Sorting Array” problem on the Leetcode. We can find it here: https://leetcode.com/problems/find-target-indices-after-sorting-array/
In short, we need to find all indices of elements in the sorted array which values are equal to the target value. One of the conditions is that we have to return it in non-decreasing order. This can be achieved using some modification of binary search. The next code can be used to return the index of the leftmost element which value is equal to the target value:
LEFT = 0
RIGHT = LENGTH(ARRAY)
WHILE LEFT < RIGHT DO
MIDDLE = (LEFT + RIGHT) / 2
IF ARRAY[MIDDLE] < TARGET THEN
LEFT = MIDDLE + 1
ELSE
RIGHT = MIDDLE
END IF
END WHILE
RETURN LEFT
We can find golang code here (binary_search_leftmost.go): https://github.com/emikhalev/algorithm/tree/master/algorithms/binary_search . We need to pay attention to the fact that if there is no target element in the array, return value (LEFT) can be unexpectable, so we need to check such case (see second return parameter).
To solve the problem with the binary search algorithm we need to sort it in non-descending order first. As we do not consider sorting algorithms in this article we can use standard library sorting solutions (for golang it’s https://pkg.go.dev/sort#IntSlice). The usual time complexity for sorting algorithms is O(N*logN).
After that we have to use binary search to find the leftmost element that is equal to the target. The time complexity for this stage is O(logN).
As soon as we have found such an element we can simply iterate over the array until we reach the element that is not equal to the target or until we reach the end of the array. The time complexity is O(M) where M is the number of elements which values are equal to the target.
SORT(ARRAY)
LEFT = 0
RIGHT = LENGTH(ARRAY)
WHILE LEFT < RIGHT DO
MIDDLE = (LEFT + RIGHT) / 2
IF ARRAY[MIDDLE] < TARGET THEN
LEFT = MIDDLE + 1
ELSE
RIGHT = MIDDLE
END IF
END WHILE
RESULT = []
WHILE LEFT < LENGTH(ARRAY) AND ARRAY[LEFT]==TARGET DO
APPEND(RESULT, LEFT)
LEFT = LEFT + 1
END WHILE
We can find the golang implementation: https://github.com/emikhalev/algorithm/blob/master/leetcode/find_target_indices_after_sorting_array/find_target_indices_after_sorting_array.go
Conclusion
As we can see the binary search algorithm looks easy but contains a lot of pitfalls. As it can be used in many solutions to computer problems it is important to understand how it works.


Top comments (0)