Introduction
I put a schedule to start GO , Algorithms and DS also advanced one with job preparation (and maybe competitive not sure yet) , Clean Coding Series , Linux (first I will start with Unix Design book ).
And the DevOps journey that I already start will be every 2 days new tutorial.
In Case your wondering who is this man in the banner it's the Khwarizmi the inventor of algorithms concept.
Make sure to follow because I will start more advanced series in future.
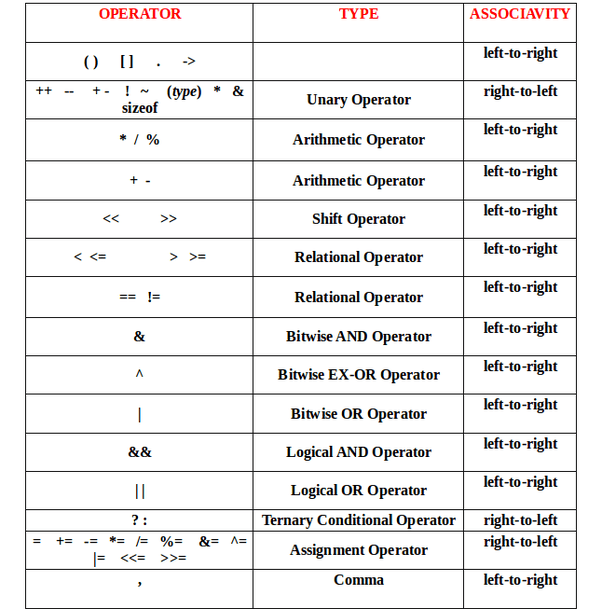
Operators in C
For example, x = 7 + 3 * 2; here, x is assigned 13, not 20 because operator * has a higher precedence than +, so it first gets multiplied with 3*2 and then adds into 7.
Here, operators with the highest precedence appear at the top of the table, those with the lowest appear at the bottom. Within an expression, higher precedence operators will be evaluated first. -- source
Arrays
One Dimensional Array
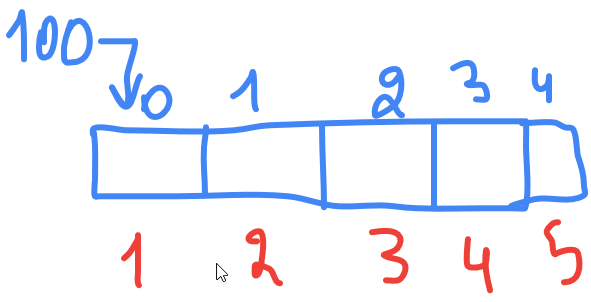
in Arrays you can random access the array by an index A[i] , in Linked Lists you can't
in order to calculate the adress of A[i] we need to know 2 informations 1 is the size of our type and the base adress of the array , those are the compiler job not us but they are good to know.
address of A[i] = i * sizeof(element) + base_address // in our example base adress is 100
address of A[i] =(i-1)* sizeof(element) + base_address // i-1 if it's start from 1 not 0
sizeof(element) depends on the type in case of integers it's 4 byte (4*8 = 32 bit)
Two Dimensional Arrays
if we understand how we can store two dimensional arrays in memory we can write better programs which they are faster
let's take this example of an 2D array with 3 rows and 4 columns
A[3][4] === A: 3x4
0 1 2 3
0 [00,01,02,03]
1 [10,11,12,13]
2 [20,21,22,23]
it gonna be complex if the compiler need to use a Linked List to link the rows with columns
so the compiler is going to transform it to one dimensional array , we have 2 methods to do so.
1 : Row major order
after transformation the array will look like this
{00,01,02,03,10,11,12,13,20,21,22,23}
if I need to reach an element I know the address of it by
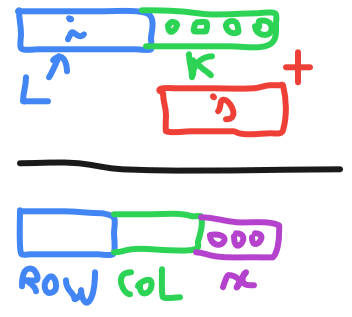
address of A[i][j] = (((i-start)*N)+(j-start))*size+B
/*
this in case of M rows and N columns
N : number of columns
i : row
j : column
start: where array start (usually 0)
size : sizeof(element)
B : Base address
*/
2 : Column major
{00,10,20,01,11,21,02,12,22,03,13,23}
address of A[i][j] = (((j-start)*M)+(i-start))*size+B
/*
this in case of M rows and N columns
M : number of rows
i : row
j : column
start: where array start (usually 0)
size : sizeof(element)
B : Base address
*/
We can also do an Binary addressing of 2D Array , wich is super complicated:
assume it's start from 0 and Row major order
{00,01,02,03,10,11,12,13,20,21,22,23}
address of A[i][j] = (i*2^K+2^L)*2^X+B // Base we also convert it to binary
N = 2^K , 0 <= i <= 2^L - 1 // L is number of binary occupied by N
M = 2^L , 0 <= j <= 2^K - 1 // K is number of binary occupied by M
i*2^K -> i will be shifted by K bits
it will occupy in memory L+K+X bits
Note : 2^X * 2^Y + 2^Z = 2^(x+Y)+2^Z
Note : if the organization is row we implement row , if it's column we implement column. Because it will give us performance.







Top comments (7)
An address is a pointer value, so when adding to it, the size is already factored in.
Which means that &A[i] is equivalent to A + i.
The only way that your formula works if it you're working with char *, in which case you'll get the wrong kind of pointer back at the end.
Beyond that, C doesn't have a flat memory model, so you can't just pretend that pointers are integers.
C does not support two dimensional arrays -- but it does support arrays of arrays.
So there's no need to transform it to a one dimensional array -- it already is one dimensional.
Indexing an array of arrays is simple pointer arithmetic.
Just as array[i] is (array + i), so is array[i][j] is *((array + i) + j).
It's a bit unclear to me why you're going out of your way to make this slower and more complicated. :)
Hi thanks for your comment ,
When you put A+i the compiler will convert it to A + (i*sizeof(element)) ,
for multi dimensional arrays yes they exist in C you can look at page 99 , section 5.7 of the original Ainsi C written by the Author of C.
But they are not the only way to do it, if you open in page 101 there is a section for Multi arrays vs pointers.
Tomorrow I will write about pointers :)
I am assuming that we don't know what is a pointer yet.
What he refers to as a multidimensional array is a one dimensional array of arrays.
Provide an example of something that you think is not a one dimensional array in C, and I will happily demonstrate to you why it is a one dimensional array. :)
If you don't know what a pointer is, you cannot meaningfully talk about arrays (since pointers are how you index arrays) or addresses (which are pointer values).
Can you give me an academic resource to read it?
Also check this one lysator.liu.se/c/c-faq/c-2.html
Sure: open-std.org/jtc1/sc22/wg14/www/do... 6.5.2.1 Array subscripting
Lysator is generally confused about arrays -- consider the mess it makes of 2.14 which is a pointer into an array of int *, rather than being multidimensional.
The simplest proof is this.
Therefore array is an array of length 3 with an element type of int[4].
Note the single dimension used to access it here.
Of course, having accessed array[i], you can now access that one dimensional array via array[i][j], and so on.
Probably the easiest way to think about it is that C provides arrays of arrays, which is one way to implement multi-dimensional arrays, without any of the arrays actually being multi-dimensional.
it's all semantics there is no such thing as truly multidimensional arrays as all arrays are one dimensional
you can use a 2 or n dimensional accessor but that's about it.
there is no need to layer a simple thing to look complex.
There are such things are truly multi-dimensional arrays, just not in C.
For example, in pascal
Or in Common Lisp
This is not a criticism of C -- deciding to use arrays of arrays rather multi-dimensional arrays is a perfectly reasonable design choice.
It's just a design choice that should be understood clearly. :)