Sometimes it is not enough to know if two strings are equals or not. Instead, we need to get an idea of how different they are.
For example, ant and aunt are two different words. However, not as different as ant and antidote. The “edit distance” between ant and aunt is smaller than the “edit distance” between _ant and antidote. _ By edit distance, I mean the number of edits (removals, inserts, and replacements) needed to turn one string into another.
In this post, I share an implementation of the Levenshtein’s algorithm that solves the edit distance problem.
The Levenshtein Algorithm
In 1965, Vladimir Levenshtein created a beautiful distance algorithm. Here is a C# implementation.
using System;
public static class Levenshtein
{
public static int Compute(string first, string second)
{
if (first.Length == 0)
{
return second.Length;
}
if (second.Length == 0)
{
return first.Length;
}
var d = new int[first.Length + 1, second.Length + 1];
for (var i = 0;
i <= first.Length;
i++)
{
d[i, 0] = i;
}
for (var j = 0;
j <= second.Length;
j++)
{
d[0, j] = j;
}
for (var i = 1;
i <= first.Length;
i++)
{
for (var j = 1;
j <= second.Length;
j++)
{
var cost = (second[j - 1] == first[i - 1]) ? 0 : 1;
d[i, j] = Min(d[i - 1, j] + 1, d[i, j - 1] + 1, d[i - 1, j - 1] + cost);
}
}
return d[first.Length, second.Length];
}
private static int Min(int e1, int e2, int e3) =>
Math.Min(Math.Min(e1, e2), e3);
}
And here it is some tests to ensure this implementation works:
public class LevenshteinShould
{
[Theory]
[InlineData("ant", "aunt", 1)]
[InlineData("fast", "cats", 3)]
[InlineData("Elemar", "Vilmar", 3)]
[InlineData("kitten", "sitting", 3)]
public void ComputeTheDistanceBetween(string s1, string s2, int expectedDistance)
{
Assert.Equal(expectedDistance, Levenshtein.ComputeDistance(s1, s2));
}
}
How it works
Levenshtein is a dynamic programming algorithm.
The main idea is to fill the entries of a matrix m, whose two dimensions equal the lengths of the two strings whose the edit distance is being computed.
At the end of the execution, each entry (i, j) holds the edit distance between the strings consisting the first i _ characters of the first string and first _j characters of the second string.
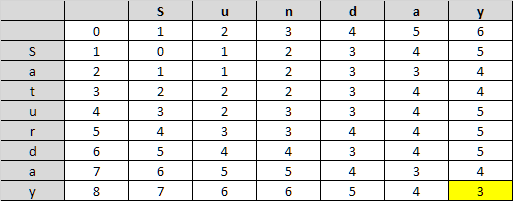
Let’s see an example:
As you can see, the cell at the bottom-right position contains the edit distance for the two string that we are comparing.
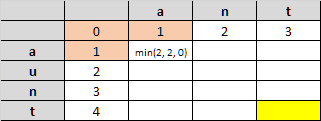
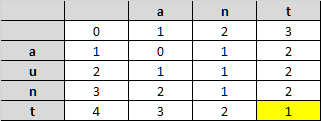
Let’s see how the algorithm works, step-by-step. This time let’s compare the strings “ant” and “aunt” (edit distance = 1)
To get started we can quickly fill the first row and column.
Then, for each cell we will compare the corresponding character from the first string and the second string, then select the minimum one of these three values:
- the value of the left cell plus one
- the value of the cell above plus one
- The value of the cell on the left and above, plus one if the characters being compared are different
And the process will continue filling the matrix.
Optimization Opportunity
As you probably noted in the step-by-step process. We only use two rows of the matrix to compute each cell value. So, we don’t need to keep all the costs, all the time, in memory.
using System;
public static class Levenshtein
{
public static int ComputeDistance(string first, string second)
{
if (first.Length == 0)
{
return second.Length;
}
if (second.Length == 0)
{
return first.Length;
}
var current = 1;
var previous = 0;
var r = new int[2, second.Length + 1];
for (var i = 0;
i <= second.Length;
i++)
{
r[previous, i] = i;
}
for (var i = 0;
i < first.Length;
i++)
{
r[current, 0] = i + 1;
for (var j = 1;
j <= second.Length;
j++)
{
var cost = (second[j - 1] == first[i]) ? 0 : 1;
r[current, j] = Min(r[previous, j] + 1, r[current, j - 1] + 1, r[previous, j - 1] + cost);
}
previous = (previous + 1) % 2;
current = (current + 1) % 2;
}
return r[previous, second.Length];
}
private static int Min(int e1, int e2, int e3) =>
Math.Min(Math.Min(e1, e2), e3);
}
Much, much better!
Last words
Levenshtein is a very interesting and robust algorithm. In the future, I will use this implementation to improve the querying experience in the simple search library that I have been working.
Again, if you have any suggestions, feel free to share it in the comments.
The post Computing the Levenshtein (Edit) Distance of Two Strings using C# appeared first on Elemar JR.





Top comments (0)