Learning Haskell programming language is essentially thinking about function application. Like mapping abstract space, minimal symbols in a page, a terminal, an editor window, I read from left to right, but then also from right to left, there is simply more dimensions than just the usual linear row of letters introducing meanings. So I'm thinking like how these functions move and what kind of transformation is happening, how definition bodies fold, which equivalences hold. Like all the time. Simply amazing, looking at the Haskell code at the bottom of the ocean of white emptiness we might notice that white space between variables, between these symbols is more than just empty space, something what merely separates letters, as in white space separating letters of some alphabet. It takes time to appreciate the shocking fact that emptiness is designating the action of function application, like the highest operator requires no space, more, it consumes it, giving it an invisible sign.
Let us observe together some of these movements:
What is the difference between fmap and map? Here we see the movement of the function shown, but how are map and fmap defined?
map _ [] = []
map f (x:xs) = f x : map f xs
fmap id = id
fmap (g . h) = (fmap g) . (fmap h)
OK, so fmap seems like a composition of two *maps, also looking at the identity fmap looks safer than map since map returns the same thing what was given, while fmap has some type of identity on itself, composition being defined as relation between two functions (g . h). Reading g after f, notice the movement from left to right while after is written before, meaning we are reading from left to right, our eyes following from g to h while in our minds we are parsing it as g coming after h, almost as if it was supposed to be written h . g.
Because everything in Haskell is pure and lazily evaluated I often lose myself pondering what is purity, what makes a computation. So again I go back to observing the monadic realm, so essentially a monad is a type of a functor, and a functor is a mapping between objects. So what is a functor? Mathematicians define a functor as a map between two categories. So why is it not called a map?
map function, found in many functional programming languages, is one example of a higher-order function. It takes as arguments a function f and a collection of elements, and as the result, returns a new collection with f applied to each element from the collection.
There is a lot of mappings in functional programming languages, it is like the defining characteristic of functional thinking, functional programming paradigm, to map a function from input to output, and there seems to be something intuitive in realizing the act of mapping itself as an aspect of computation. Other functions like map are filter or fold, which are like kinds of mappings we can do, for instance filter is a function that filters some relation out from a domain of relations. These are all higher-order functions, meaning their output, the value they realize could be just another function.
In Haskell, a function is a mapping that takes one or more arguments and produces a single result, and is defined using an equation that gives a name for the argument, a name for each of its arguments, and a body that specifies how the result can be calculated in terms of the arguments.
I remember being awe struck the first time I read this definition from Programming in Haskell by Graham Hutton. There is something strange about it. It feels pure by not having any operational words, no commands, no instructions. It is somehow contained within itself, not dealing with the outside world, it is just a description of an action. Hutton continues:
For, example, a function
doublethat takes a numberxas its argument, and produces the resultx + x, can be defined by the following equation:
double x = x + x
double 3
= { applying double }
3 + 3
= { applying + }
6
-- other examples:
area r = pi * r^2
But the super cool thing is these arguments can be other functions too, and what one ends up with is applying or processing functions until the very atoms emerge, elements like numbers or words and we get the final value, the final output of our functions. What is nice is the fact that data is not lost in between, it is not under the table, but it is openly outside, each function producing a unique value which is passed on to another function. When we pass around functions into functions we have higher-order functions.
So is every function a functor? How is functor defined mathematically? Let C and D be categories. Now these two categories are like two collections of a bunch of objects, and the notion of a category is like a minimal definition of some group of objects, or just one object. It has an identity and associativity, basically it has two operations defined, included among them to even form a minimal bunch of objects. Just think about, how would you define a group of objects, how would you even imagine a group of objects? There has to be some kind of identity, at least the very act of realizing there are some objects includes some notion of identity, something passed on, something given.
class Functor f where
fmap :: (a -> b) -> f a -> f b


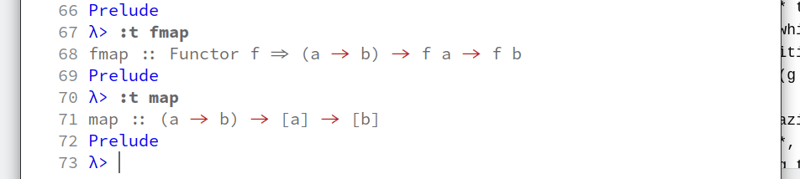






Top comments (0)