(my newsletter subscribers received this first)
In the last issue, we talked about 'Breadth-First Search' and 'Depth-First Search' as two of the most common algorithms we use when working with graphs.
Last time, we looked at Breadth-First Search (BFS).
Today, we'll cover the other, Depth-First Search (DFS).
Why should I care?
A lot of algorithms are implemented for you as part of your chosen language. That means that they are interesting to learn about, but that you'll
rarely write them yourself.
Graph traversal algorithms are different.
We use graphs all the time, from linking related products in an e-commerce application to mapping relationships between people in a social network.
Searching a graph is something that is not only useful in theory, but that you will almost certainly need to do in practice too.
In 5 minutes or less:
Here's a graph data structure:
The 'nodes' in the graph (A-F) are called 'vertices'. Each vertex is connected to one or more others with 'edges', which are the lines between the nodes.
But a graph is only useful if we can do something with it; we might want to find out whether a certain element is stored in our graph, or how many 'hops' it takes to get between two elements.
These kinds of problems are called 'graph traversal', and 'Depth-First Search' (or 'DFS') is one algorithm to do this.
Let's take a look...
How Depth-First Search works
In this issue, we looked at the 'stack' data structure.
You'll recall that it is a 'First In Last Out' data structure; the first item to be added to the stack will be the last item to be removed:
The stack is the basis for Depth First Search.
Here's a summary of the algorithm:
- Pick any unvisited connected node, add it to the stack, and mark it as 'visited'
- From the node we just picked, do the same thing again.
- Repeat until we end up at a node with no unvisited connections
- Pop the top item from the stack, and repeat the whole process again from the next item down
- When the stack is empty, we're done!
This sounds much more confusing than it is in practice, so let's walk through an example...
Implementing DFS
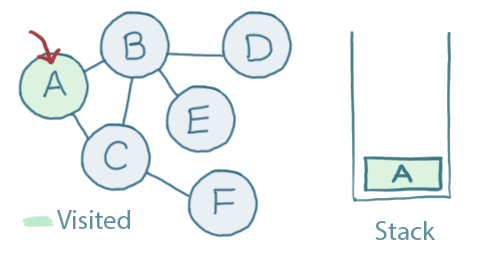
We start by picking a place to start, we'll choose A.
The first step is to add A to the stack and mark it as 'visited':
Now, we need to repeat the following steps:
- Pick any unvisited connected node, add it to the stack, and mark it as 'visited'
- From the node we just picked, do the same thing again.
- Repeat until we end up at a node with no unvisited connections
So, let's pick a connected node and get started.
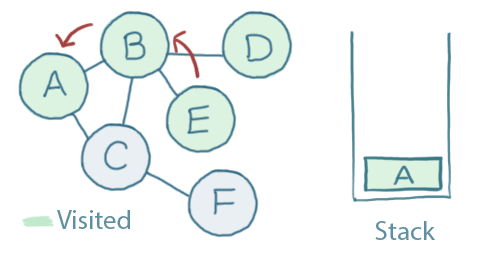
Both B and C are connected to A. We haven't visited either, so we can pick either one to visit next. Let's pick B.
From B, we can either visit A, D or E. We've already visited A, so we ignore that one. Let's pick D.
We add D to the stack and mark it as 'visited', just like we did before:
From D there are no unvisited nodes to visit. It's only connected to B, and we've just been there.
So, now it's time to do this:
- Pop the top item from the stack, and repeat the whole process again from the next item down
We'll pop D off of the stack and go back to the node underneath it.. which is B.
Now we're back at B, we'll just do the same thing all over again...
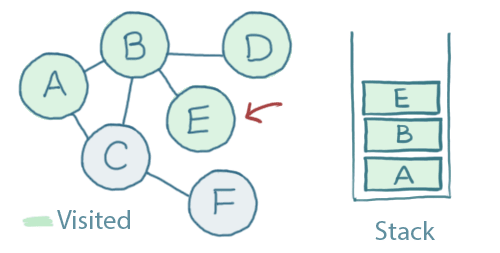
There's one unvisited node - E - so we'll visit it and add it to the stack:
E has no unvisited neighbours. When we pop that off of the stack we'll see that neither does B, so we pop that one off too:
That has brought us right back up the top of the graph again, to A.
I'm sure you have the hang of this by now; we'll keep picking an unvisited connected vertex and adding it to the stack.
After adding C and F in that way, this is what the stack looks like:
Since F has no unvisited connections, we pop it off of the stack. The same will apply to the next item down - C - and then A.
That leaves us an empty stack, meaning we're done!
Applications of DFS
The DFS algorithm is useful when we are looking for an item that we know is likely to be at the bottom of the graph. Unlike Breadth-First search, DFS dives straight to the bottom of the graph, before working its way back up.
Imagine we have a family tree, and we're looking for the youngest member. We know they're going to be at the bottom of the tree, so DFS might be a better choice in that case.
In cases where the item you are searching for is likely to be at the top of the graph, consider 'Breadth-First search'. When the item is likely to be nearer to the bottom, consider 'Depth-First search'
Want to know more?
Check out these links:









Top comments (0)