So its more or less Christmastime and I was reminded the other day of a popular childrens puzzle in German-speaking countries called Haus des Nikolaus which roughly translates to House of Santa Claus1.
Being a child I always solved it with one solution I had memorized but only a few years ago I learned about the theoretical basis of it during a university math class by accident.
So having a little downtime and thinking it could be fun, welcome to my first ever post on the internet!
The puzzle is to draw a house like the one in the title image, beginning in any one of its corners, never retracing a line you've already drawn and never lifting your pen.
The end result should look like this:
Take out a piece of paper and try it! Can you solve it? Can you think of multiple solutions to the problem?
Did it? Couldn't do it? I came here to read not to draw!?
Let's see how we can formalize and solve the problem using graphs!
For starters let's have some definitions
A graph consists of a set of nodes (or vertices) and edges connecting them. In our special case we are talking about an undirected graph, ie. a graph in which you can traverse the edges in either direction.
Another definition we have to make is the degree of a node, ie. the number of edges connected to a node.
So with our new knowledge let's setup santa's house as a graph with each node's degree denoted next to it.
Brief course in history
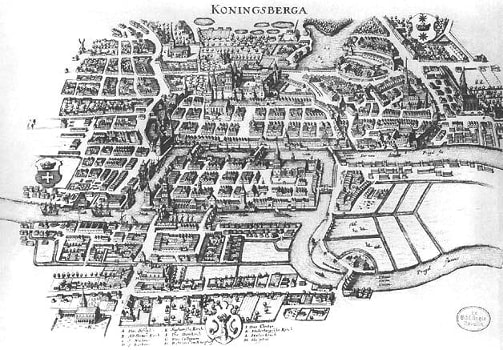
The Haus des Nikolaus problem could be interpreted as a variation of an early 18th century problem, the Seven Bridges of Königsberg, addressed by mathematician Leonhard Euler (1707-1783).
The question was whether it was possible to devise a round-trip through the then capital of East Prussia, the city of Königsberg, crossing all of its seven bridges exactly once and end up where you started your trip.
Euler's solution to the problem is today regarded as the first ever published paper on graph theory.
He observed that when you enter a landmass coming across a bridge you must also exit that landmass using a bridge. Since you aren't allowed to use the same bridge twice for either entering or exiting, each landmass must have an even number of bridges connected to it. One for entering and one for exiting the landmass.
He concluded that the Seven Bridges of Königsberg problem has no solution because each of the landmasses had an odd number of bridges connected to it.
To state the problem and Eulers observation more generally:
Find a way through a graph that
1) visits all nodes,
2) traverses every edge exactly once,
3) and starts and ends in the same node.
This way is called a Eulerian cycle.
An undirected graph has a Eulerian cycle if and only if every node has an even degree.
For a more complete and coherent post about the Seven Bridges of Königsberg problem check out Vaidehi Joshi's awesome post on it!
Back to our house
The constraints for our house drawing stated earlier can be rephrased as a weaker variation of the Eulerian cycle:
Find a way through a graph that
1) visits all nodes,
2) traverses every edge exactly once,
3) BUT start and end node need not be the same.
This way is called a Eulerian trail.
From our observations above we can derive that a Eulerian trail is present in a graph if and only if exactly zero or two nodes have an odd degree.
As we can see from our Haus des Nikolaus graph representation luckily we have exactly 2 nodes with odd degree in our graph so we can conclude that a solution is in fact possible!
But there's a catch.
The only way you can make your drawing work is when you start and end your path in one of the odd degree nodes.
To make this fact more apparent, let's tag each edge with either 'in' or 'out' depending on which direction you want to use them in your path.

Now we can immediately see that one of the bottom nodes has 2 inputs but only 1 output, meaning you'll inevitably end up getting trapped in it. This naturally must be your end node.
The other of the two bottom nodes has 2 outputs but just 1 input, meaning that in order to traverse all the edges in the graph one of the 2 outputs needs to be the first edge you traverse. Making that node your start node.
So there we have it. A simple childrens puzzle solved with far too much effort!
I have the feeling that this is the kind of useless information that tends to stick with you forever. Also it's always interesting to encounter and identify variations of famous mathematical problems in the wild.
Hope you had fun :)
Extra Credit
How many possible solutions to this problem are there?
1 That's a lie Nikolaus does not translate to Santa Clause. He is Saint Nicholas. The rhyme just works better like that :P







Top comments (3)
Now do the same but without the top triangle
Haha you'll be there for a while :P
congrats to your first post! I'm so proud 😍