Quick Start to Priority Queue and Heap | With Python

Priority Queue

Starting with Priority Queue, let’s first understand what a simple queue is and how it is different from a Priority Queue.
Can think of a line where you had to stand, waiting for your turn to get your Pizza, or may be to get into a bus? That is a queue you are standing in. A simple queue, where the first person who joined it, will be the first one to leave it too. Hence, a FIFO (or First In First Out) linear data structure.

Now imagine, what if in that same queue, a celebrity joins in? Or may be the President of your country? Would that person be standing at the end of the queue now to wait for his turn? Well, in this circumstances, you might want them to go before you, despite the fact they joined last.

This is a priority queue where each data in the queue has a certain priority and the data with highest priority goes out first and then the second and so on.

Implementation

From the above example, it can be seen that a simple queue cannot be used to implement a priority queue, where each data is associated with some weight. So far, priority queue is just like an Abstract Data Type which has to be implemented separately to get the desired order.

Note: Priority queue only supports the data which can be compared with each other. That is, it should be possible to order the data from least to highest priority or highest to least priority.
A classic implementation of Priority Queue can be with Binary Heap.

Binary Heap

As the name suggests, in a binary heap, every node has at most two children. Sounds similar to Binary Tree? Well, Binary heap is a special kind of binary tree where the ordering of every nodes matter. In which way, let’s find those below:

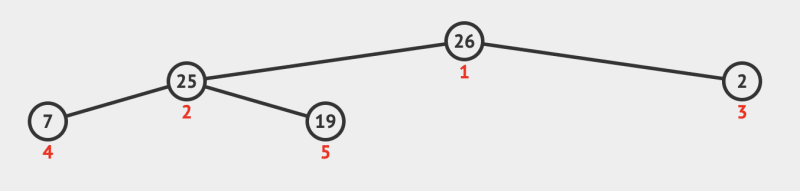
• Each Node has higher priority than its children’s. In the below diagram, the red coloured numbers represent the priorities of the nodes.

• Every heap is a complete binary tree, meaning each level in the tree should have the maximum number of nodes, except the last level.

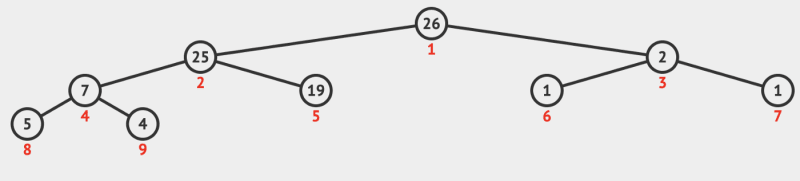
• Insertion of new Node always happens from left to right and only in the last level (or new next level when the last level is complete). In case of violation of the Heap Property after insertion, swapping must takes place to satisfy it. For example, if we try to insert 4 to the above valid heap:

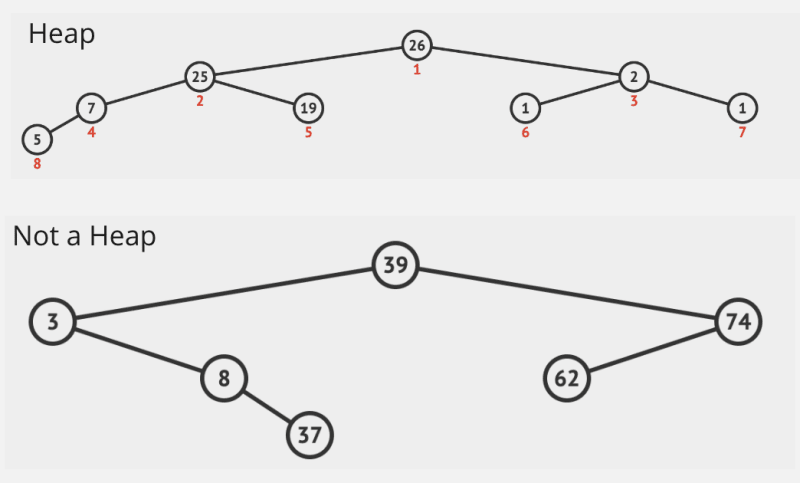
• There are two types of Heaps:

1. Max Heap — In this, nodes are ordered from larger values in the top levels to smaller values in the lower levels.
2. Min Heap — In this, nodes are ordered from smaller values in top levels to larger values in lower levels.

• The root node of a Heap always contains the element with highest priority or greatest value in case of Max heap or lowest value in case of Min heap, which is removed first when popped from the Heap.

Representations of Heap:

A Heap can be typically represented with an array.

The above Heap can be represented as :

Now some points to note from the array implementation:

• Here we can clearly see that for each node at index i, the children nodes are at (2*i + 1, 2*i +2)

• Parent of a node at index i is (i-1)//2

• To distinguish between Leaf and internal nodes, we have : if n is the length of the array, then any node at index i is internal if 2*i+2 <= n. Else it is a leaf node.

Operations on Binary Heap

We can now implement Priority Queue requirements with the help of a Binary heap but in extreme rare occasions, we will need to write the entire implementation from scratch by ourselves. Since already lots of libraries in most of the programming languages offer pre-built Heaps , knowing how it works and how to use the implementations to get our desired output often suffice.

In this article, we will go through the Python 3 library, heapq, for Heap implementation and get an overview of what their major functions do.

Heapify:

Starting with Heapify, it is the process of creating a heap data structure from a binary tree. Both Min-Heap or a Max-Heap can be created with this process.

This process is also used internally to maintain the heap property after insertion or deletion of a node. Time complexity of the process is O(logn).

Heap Pop or Delete:

This is the process of popping out element from the Heap, in which always the root node gets deleted first.
The deletion starts with replacement of the last element with the root node to be deleted and then heapifying the last node in its correct index.

This process uses PercolateDown approach and the Time complexity is O(logn).

Heap push or Insertion:

This is the process of inserting new value into the Heap, which always happens at the last level, from left to right order. In case of violation of the Heap property, heapifying the tree may takes place and the process uses PercolateUp approach with a time complexity of O(logn).

A simple Python Implementation

from heapq import heappush, heappop,heapify

heap = [26,19,7,4,2,25,5,1,1]
heapify(heap)

print("The heap is :\n>>> ",heap)
heappush(heap,9)

print("After inserting 9 \n>>> ",heap)
root = heappop(heap)

print("The popped value: ",root)
print("The left over heap: \n>>> ",heap)

Note: By default, the heap created is min-heap. in case max-heap implementation is needed, we can use this library instead or multiply our value with -1:

https://pypi.org/project/heapq_max/

Hope it helps to get started with Heap. Cheers! 😊