You are probably familiar with arrays, stacks and linked lists which are linear data structures because they store the data in a sequence. Graph is a non-linear data structure just like a tree data structure. In fact tree is a special kind of data structure with some restrictions.
Graphs have a lot of real world applications like finding the best routes in navigation apps, creating complex electrical circuits, storing useful user information on social media platforms, etc.
Before moving forward we must know the following terms:
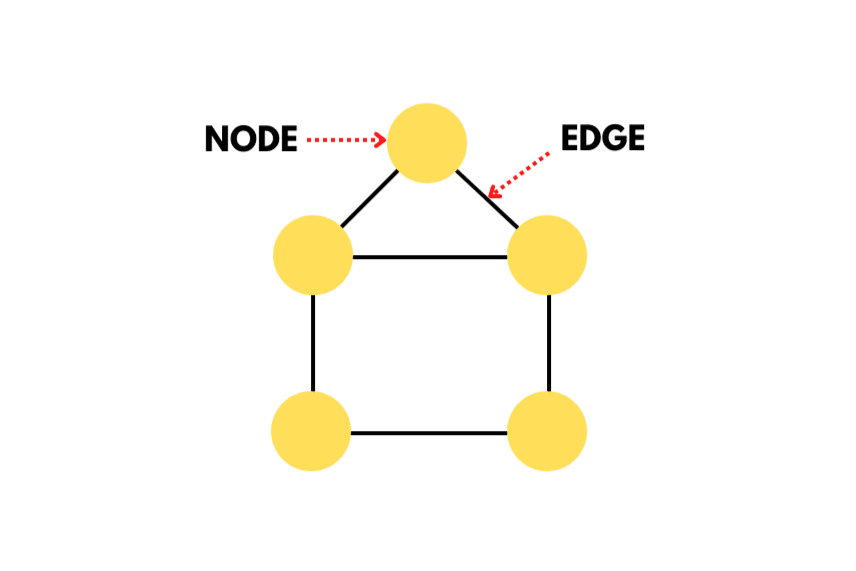
Nodes: These are the vertices of the graph that are used to store the data and are connected by edges.
Edges: Two nodes are connected by a horizontal line called an edge. An edge can be directed or undirected. A directed edge means that we can only traverse the graph in one direction which is shown by the edge whereas an undirected edge lets us traverse in any direction.
Graphs are of two types:
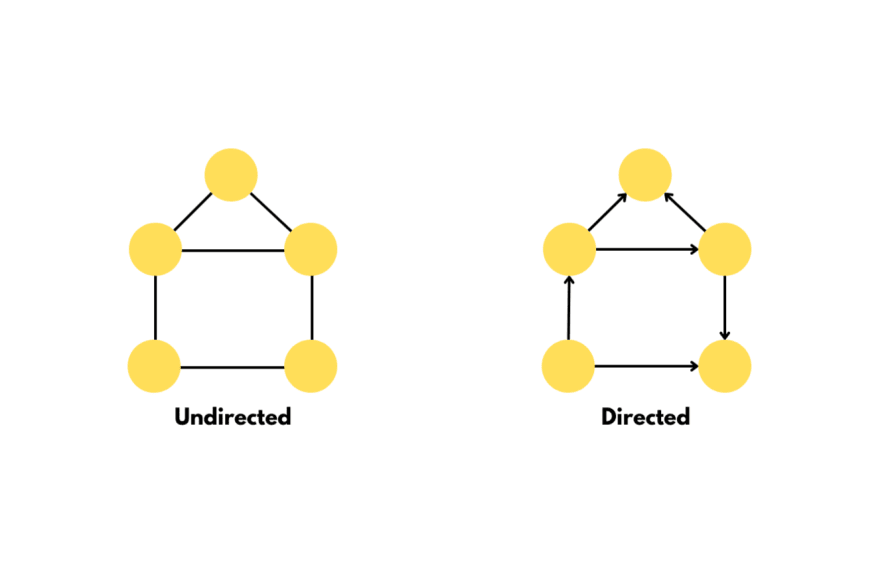
- Undirected graph: A type of graph in which the nodes are connected by undirected edges.
- Directed graph: A type of graph in which the nodes are connected by directed edges.
Cycle in a Graph
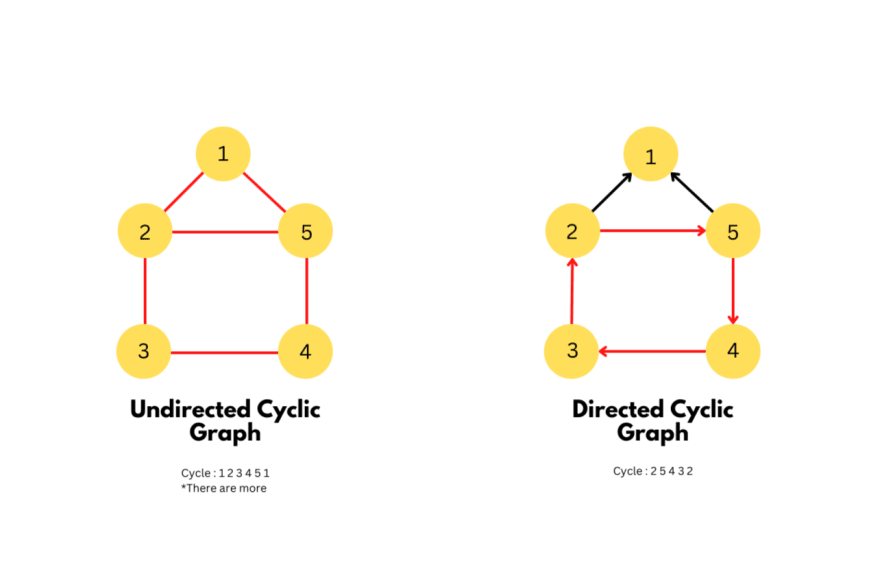
When we start moving from one node and after a few moves end up back at the starting node, this means that there's a cycle in the graph.
If there is a cycle in a graph and the edges are undirected then the graph is called Undirected Cyclic Graph.
Similarly if the graph has a cycle but the edges are directed then it's called a Directed Cyclic Graph.
Degree of a Graph
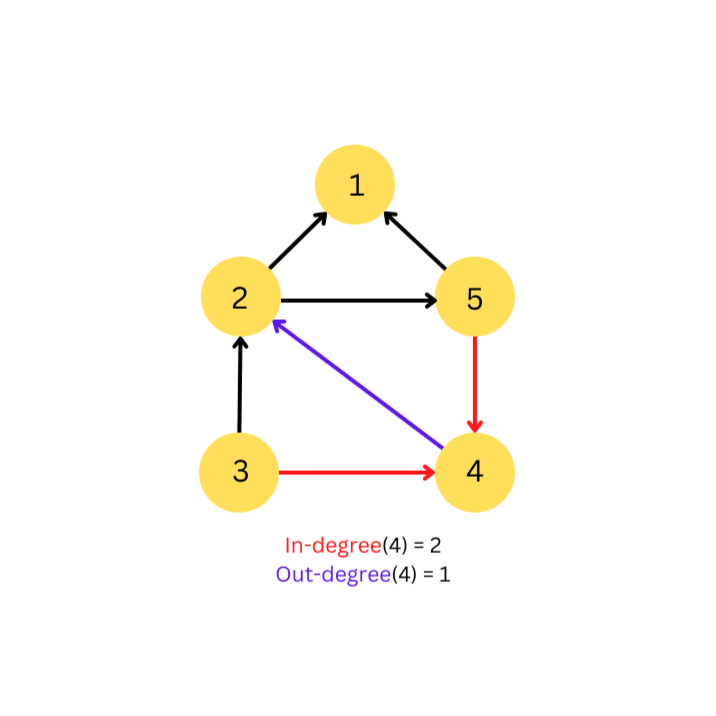
In case of undirected graphs the number of edges connected to a node is it's degree.
But in Directed graphs:
In-degree: Total number of incoming edges in a node.
Out-degree: Total number of outgoing edges in a node.
Total degree of a graph = 2 x the number of edges in the graph
Weights in a Graph
Weights are used to measure the cost of a traversal in a graph usually represented by edges hence known as weighted edges.
Why do we need them? Well consider this, you have to travel from city A to city B but there are multiple paths that you can use. To make the decision easier we can just calculate the time it'll take for us to reach our destination for each path and then pick the one with lowest time.
That's about the introduction to graphs but there are a lot of interesting and important topics associated with graphs like representing a graph in a language, traversal algorithms, shortest path algorithms, cycle detection algorithms, topological sort, etc.
I hope this article was helpful for you.
Thanks for reading.



Top comments (0)