Background
When I learned to code, I hadn’t slept in a math classroom in 14 years.
I studied philosophy and taught courses on Symbolic Logic. I can talk about deductive proofs for days, but when people pull out a f of n’s… x²… [insert Greek letter] — I nod along, but trust me, I have no idea what’s happening.
For this reason, I got a huge boost when I figured out an algorithm question asking, “How can you determine the mathematical combination (nCr) of two numbers?”
If you’re like ‘what the…?’, then hell yeah, you are me a day ago. Let’s go!
The Meat
Defining the Problem
I’ll try my best to explain a combination:
Imagine you’re losing a high stakes poker game. You have sweat on your neck as a couple Mafia grunts stare daggers at you. As the big one cracks his knuckles, you think “It’s a shame I never learned to count cards. But maybe start now?”
Your mind races. You think, how do I start? How many hands are there in the deck?
There’s 52 cards. You get 5 distinct cards in each hand, and they can come in any order. Let’s see, some quick math in your head and…
Yeah, the answer is not obvious. But, you’re attempting to find a combination. A combination is when you have a collection of items and you want to find all the possible selections from that collection — for example, every possible hand from a deck of cards.
By the way, the answer is 2,598,960. Each hand has a 1/2,598,960th chance of being drawn.
With numbers that big, it’s good we can train a computer to solve the problem.
Solution
The mathematical formula for finding a combination looks like this:
The Ruby version looks like this:
def factorial(num)
(1..num).inject(1){ |prod, i| prod * i }
end
def get_combination(num1, num2)
factorial(num1) / (factorial(num2) * factorial(num1 - num2))
end
Explanation
Okay, let’s break it down. The math works like this:
- On top, we have
n!. First, we find the factorial of our collection. - Next, we subtract our selection from the collection and find the factorial of that or
(n — r)!. - Find the factorial of our selection
r!and multiply by the result of step 2. - Finally, divide step 1 —
n!— by the result of step 3 —r!(n-r)!.
Let’s translate it to Ruby
1 . Ruby does not have a method for finding a factorial so we have to write one. I found a couple nice one-liners here and here.
def factorial(num)
(1..num).inject(1) { |prod, i| prod * i }
end
A factorial is the product of an integer and all the integers below it. So, if we wanted to know the factorial of 3 or 3!, we calculate 1 * 2 * 3 and get 6.
Abstracting this with Ruby, inject will be a useful method. inject among other things, can take an array of numbers and apply a block reducing them to a single number. (That’s why inject is aliased as reduce).
In this case, our array is the range of numbers from 1 to our target. We iterate through the array multiplying each number to a parameter initially set to 1, and return the result.
2 . With our factorial method written, we can find a combination in one line.
def get_combination(num1, num2)
factorial(num1) / (factorial(num2) * factorial(num1 - num2))
end
Here we are simply following the mathematical steps outlined earlier. We find the factorial of our collection, and divide it by the factorial of our set multiplied by the result of a factorial of the result of our collection minus our set. Got it?
BOOM! That's it.
Thanks for reading. Hope this helps someone!




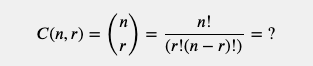





Top comments (2)
Thanks for the explanation!
As a side note, factorial can also be implemented as
(1..n).inject(&:*). We can even drop the&and make itinject(:*)only.Thanks, Jason. 👏
Your explanation helped me a lot to solve a Hacker Rank's Ruby combination challenge I was stuck for a while.