Binary Insertion Sort

Why do we sort?

Often the tasks we perform on arrays, e.g. searching, can be significantly optimized when the array is sorted.

The reason? Because we're able to find the relevant data so much faster.

Classic insertion sort looks like this.

public static void insertionSort(int[] nums) {

    for(int i=1; i < nums.length; ++i) {
        int current = nums[i], j;

        for(j=i-1; j >= 0 && current < nums[j]; --j)
            nums[j+1] = nums[j];

        nums[j+1] = current;
    }
}

We're creating a sorted window on the left side of the array, adding each new element to its correct position by linearly traversing from the window's inner (right) edge.

When an array is sorted in reverse, we observe the worst case time complexity of O(n^2) as every element needs to be compared to every other element.

Can we do better? Let's try!

Binary Insertion Sort

Analyzing the classic Insertion sort, we see it centers around 2 core steps:

1. Find the next element's proper insert position in the sorted window - O(n)
2. Make room by shifting all greater elements - O(n)

Both of these steps take linear time and are applied to every element (O(n)).

Classic Time Complexity = O(n (n + n)) = O(n^2 + n^2) = O(n^2)

Let's attempt to optimize the individual steps.

Step 1. Is there anyway we can find the insert position faster than O(n)?

• Actually yes! Since the window is sorted, we can use binary search in place of linear search to improve this step exponentially.

Step 2. Is shifting elements one by one the only way?

• Unfortunately so, however Java has a built-in System API, System.arraycopy(), which optimizes the process.

Let's look at the Java implementation for the Binary variant.

public static void insertionSortCoffeeless(int[] arr) {
    for(int i=1; i < arr.length; ++i) {
        current = arr[i];

        int j = findInsertPosition(arr, 0, i-1, current);
        System.arraycopy(arr, j, arr, j + 1, i - j);

        arr[j] = current;
    }
}

private static int findInsertPosition(int[] nums, int lB, int rB, int target) {
    int mid=(lB+rB)/2;

    while(lB<=rB) {
        mid=(lB+rB)/2;

        if(target < nums[mid]) rB=mid-1;
        else lB = mid+1;
    }

    return target < nums[mid] ? mid : mid+1;
}

Binary Time Complexity = O(n (log n + n)) = O(nlog n + n^2) = O(n^2)

After the improvements we still have a Big O of n-squared, however based on the derivation we see it should perform somewhat faster.

The bottleneck shifts from finding the correct position, to shifting all greater elements over by one.

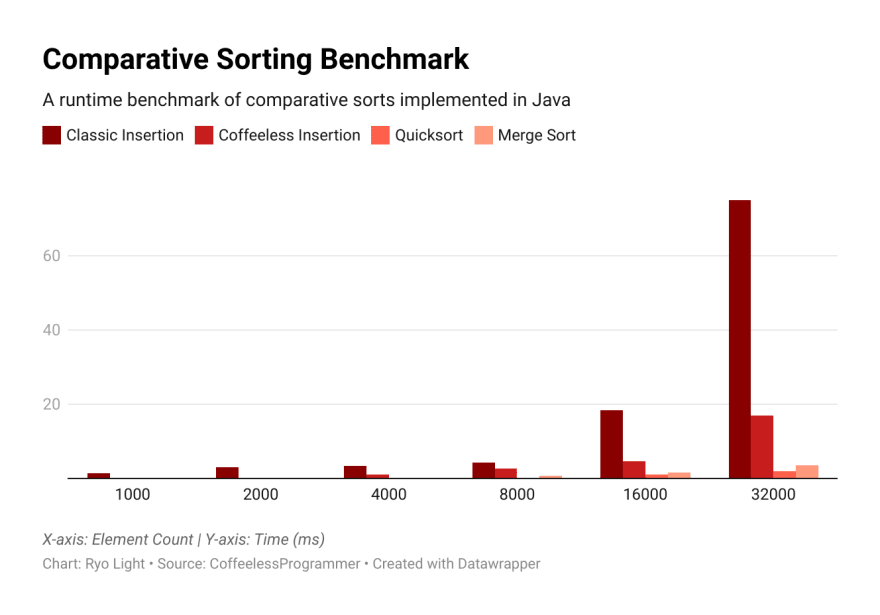
How much faster is it practically?

Below are the results of comparing common sorts on 32-bit integer arrays of increasing size.

The Binary variant remains practical (under 5 ms) for lists of up ~20,000 elements.

And if in the future, computer architectures allow a variable-length block of memory to be overwritten in constant time, we have an in-place, stable sort with a guaranteed time complexity of O(nlog n).

Until Next Time,
Ryo

References

• Insertion Sort Visual Explanation | Instagram
• System.arraycopy() | Java 17 Docs
• Insertion Sort Variants | Wikipedia